
【题目】如图,OD平分∠BOC,OE平分∠AOC.
(1)若∠BOC=60°,∠AOC=40°,求∠DOE的度数;
(2)若∠DOE=n°,求∠AOB的度数;
(3)若∠DOE+∠AOB=180°,求∠AOB与∠DOE的度数.

【答案】(1)∠DOE=50° ;(2)∠AOB=2∠DOE=2n°;(3)∠AOB=120°,∠DOE=60°.
【解析】
(1)根据角平分线定义分别求出∠COD和∠COE,即可求得∠DOE的度数;
(2)根据角平分线定义得出∠BOC=2∠COD,∠AOC=2∠EOC,求出∠AOB=2∠DOE,代入即可求解;
(3)根据∠DOE+∠AOB=180°,把∠AOB=2∠DOE代入求出即可.
解:(1)∵OD平分∠BOC,∠BOC=60°,
![]() 同理∠COE=20°
同理∠COE=20°
∴∠DOE=∠COD+∠COE=30°+20°=50°
(2)∵OD平分∠BOC
∴∠BOC=2∠DOC
同理∠AOC=2∠COE
∵∠AOB=∠AOC+∠BOC
∴∠AOB=2∠DOC+2∠COE=2(∠DOC+∠COE)=2∠DOE=2n°
(3)∵∠AOB=2∠DOE,∠DOE+∠AOB=180°
∴∠DOE+2∠DOE=180° ,
∴∠DOE=60°,
∴∠AOB=120°.
故答案为:(1)∠DOE=50° ;(2)∠AOB=2∠DOE=2n°;(3)∠AOB=120°,∠DOE=60°.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
【题目】如图,AB=AC,AD是△ABC的角平分线,DE⊥AB于E,DF⊥AC于F,则下列四个结论中:①DE=DF;②AD上任意一点到AB,AC的距离相等;③∠BDE=∠CDF;④BD=CD且AD⊥BC,其中正确的有( )
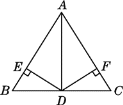
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() (a<0)图象与x轴的交点A、B的横坐标分别为﹣3,1,与y轴交于点C,下面四个结论:
(a<0)图象与x轴的交点A、B的横坐标分别为﹣3,1,与y轴交于点C,下面四个结论:
①16a﹣4b+c<0;②若P(﹣5,y1),Q(![]() ,y2)是函数图象上的两点,则y1>y2;③a=﹣
,y2)是函数图象上的两点,则y1>y2;③a=﹣![]() c;④若△ABC是等腰三角形,则b=﹣
c;④若△ABC是等腰三角形,则b=﹣![]() .其中正确的有______(请将结论正确的序号全部填上)
.其中正确的有______(请将结论正确的序号全部填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在方格纸中,点A,B,P都在格点上.请按要求画出以AB为边的格点四边形,使P在四边形内部(不包括边界上),且P到四边形的两个顶点的距离相等.

(1)在图甲中画出一个ABCD.
(2)在图乙中画出一个四边形ABCD,使∠D=90°,且∠A≠90°.(注:图甲、乙在答题纸上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数a,b,c在数轴上的位置如图所示:
![]()
(1)比较大小:b____0, a____c, b____c, b-a____0;
(2)A,B两点间的距离为__________,B,C两点间的距离为_______;
(3)化简:|b|-|b+c|+|c-a|-|a+c|-|b-c|.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B和线段CD都在数轴上,点A,C,D,B起始位置所表示的数分别为-2,0,3,12;线段CD沿数轴的正方向以每秒1个单位长度的速度运动,运动时间为1秒.
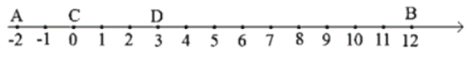
(1)当![]() =0秒时,AC的长为________,当
=0秒时,AC的长为________,当![]() =2秒时,AC的长为________;
=2秒时,AC的长为________;
(2)用含有![]() 的代数式表示AC的线段长为________;
的代数式表示AC的线段长为________;
(3)当![]() =__________秒时,AC-BD=5;当
=__________秒时,AC-BD=5;当![]() =___________秒时AC+BD=15;
=___________秒时AC+BD=15;
(4)若点A与线段CD同时出发沿数轴的正方向移动,点A的速度为每秒2个单位长度,在移动过程中,是否存在某一时刻使得AC=2BD,若存在,请直接求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
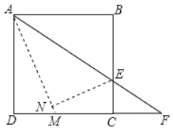
【题目】如图,正方形ABCD的边长为8,点E是BC上的一点,连接AE并延长交射线DC于点F,将△ABE沿直线AE翻折,点B落在点N处,AN的延长线交DC于点M,当AB=2CF时,则NM的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
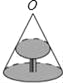
【题目】如图是圆桌正上方的灯泡O发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图.已知桌面的直径为1.2m,桌面距离地面1m,若灯泡O距离地面3m,则地面上阴影部分的面积为_____m2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com