
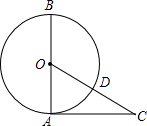
 如图,AB是⊙O的直径,AC是⊙O的切线,OC交⊙O于点D,若∠C=40°,OA=9,则$\widehat{BD}$的长为$\frac{13}{2}$π.(结果保留π)
如图,AB是⊙O的直径,AC是⊙O的切线,OC交⊙O于点D,若∠C=40°,OA=9,则$\widehat{BD}$的长为$\frac{13}{2}$π.(结果保留π)  小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:填空题
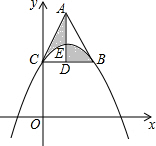 如图,在平面直角坐标系中,点C是抛物线y=a(x-3)2+k与y轴的交点,点B是这条抛物线上另一点,且BC∥x轴,以CB为边向上作等边三角形ABC,BC边上的高AD交抛物线于点E,则阴影部分图形的面积为$\frac{9}{2}$$\sqrt{3}$.
如图,在平面直角坐标系中,点C是抛物线y=a(x-3)2+k与y轴的交点,点B是这条抛物线上另一点,且BC∥x轴,以CB为边向上作等边三角形ABC,BC边上的高AD交抛物线于点E,则阴影部分图形的面积为$\frac{9}{2}$$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
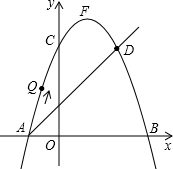 如图,在平面直角坐标系中,直线AD与抛物线y=-x2+bx+c交于A(-1,0)和D(2,3)两点,点C、F分别为该抛物线与y轴的交点和顶点.
如图,在平面直角坐标系中,直线AD与抛物线y=-x2+bx+c交于A(-1,0)和D(2,3)两点,点C、F分别为该抛物线与y轴的交点和顶点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
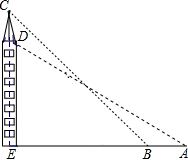 如图,在一个20米高的楼顶上有一信号塔DC,某同学为了测量信号塔的高度,在地面的A处测得信号塔下端D的仰角为30°,然后他正对塔的方向前进了8米到达地面的B处,又测得信号塔顶端C的仰角为45°,CD⊥AB于点E,E、B、A在一条直线上.信号塔CD的高度为( )
如图,在一个20米高的楼顶上有一信号塔DC,某同学为了测量信号塔的高度,在地面的A处测得信号塔下端D的仰角为30°,然后他正对塔的方向前进了8米到达地面的B处,又测得信号塔顶端C的仰角为45°,CD⊥AB于点E,E、B、A在一条直线上.信号塔CD的高度为( )| A. | 20$\sqrt{3}$ | B. | 20$\sqrt{3}$-8 | C. | 20$\sqrt{3}$-28 | D. | 20$\sqrt{3}$-20 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
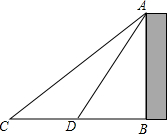 天津北宁公园内的致远塔,塔高九层,塔内四周墙壁上镶钳着历史题材为内容的瓷板油彩画或青石刻浮雕,叠双向盘旋楼梯或电梯可达九层,津门美景尽收眼底,是我国目前最高的宝塔.某校数学情趣小组实地测量了致远塔的高度AB,如图,在C处测得塔尖A的仰角为45°,再沿CB方向前进31.45m到达D处,测得塔尖A的仰角为60°,求塔高AB(精确到0.1m,$\sqrt{3}$≈1.732)
天津北宁公园内的致远塔,塔高九层,塔内四周墙壁上镶钳着历史题材为内容的瓷板油彩画或青石刻浮雕,叠双向盘旋楼梯或电梯可达九层,津门美景尽收眼底,是我国目前最高的宝塔.某校数学情趣小组实地测量了致远塔的高度AB,如图,在C处测得塔尖A的仰角为45°,再沿CB方向前进31.45m到达D处,测得塔尖A的仰角为60°,求塔高AB(精确到0.1m,$\sqrt{3}$≈1.732)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com