
 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
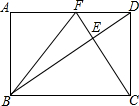 在矩形ABCD中,DC=2$\sqrt{3}$,CF⊥BD分别交BD、AD于点E、F,连接BF.
在矩形ABCD中,DC=2$\sqrt{3}$,CF⊥BD分别交BD、AD于点E、F,连接BF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,一半径为2的圆的圆心的初始位置在(0,2),此时圆上一点P的位置在(0,0),圆在x轴上以每秒$\frac{π}{3}$的速度沿x轴正方向滚动,8秒时P点到x轴的距离为3.
如图,在平面直角坐标系中,一半径为2的圆的圆心的初始位置在(0,2),此时圆上一点P的位置在(0,0),圆在x轴上以每秒$\frac{π}{3}$的速度沿x轴正方向滚动,8秒时P点到x轴的距离为3.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,4个小圆的面积相等,大圆的半径等于小圆的直径,则图中阴影部分的面积S1与大圆的面积S2的大小关系为( )
如图,4个小圆的面积相等,大圆的半径等于小圆的直径,则图中阴影部分的面积S1与大圆的面积S2的大小关系为( )| A. | S1=S2 | B. | S1=$\frac{1}{2}$S2 | C. | S1=$\frac{1}{3}$S2 | D. | S1=$\frac{1}{4}$S2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 平顶山市积极开展“节水”活动,小明利用课余时间对某小区 300户居民的用 水情况进行统计,发现12月份各户居民的用水量比11月份有所下降,小明将12月份各户居民的节水量统汁整理成如下统计图表:
平顶山市积极开展“节水”活动,小明利用课余时间对某小区 300户居民的用 水情况进行统计,发现12月份各户居民的用水量比11月份有所下降,小明将12月份各户居民的节水量统汁整理成如下统计图表:| 节水量(吨) | 1 | 1.5 | 2.5 | 3 |
| 户数 | 50 | 80 | 100 | 70 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com