练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    我们学习过二次函数的图象的平移，先作出二次函数y=2x2+1的图象．
    ①向上平移3个单位，所得图象的函数表达式是
     
    ；
    ②向下平移4个单位，所得图象的函数表达式是
     
    ；
    ③向左平移5个单位，所得图象的函数表达式是
     
    ；
    ④向右平移6个单位，所得图象的函数表达式是
     
    ．
    由此可以归纳二次函数y=ax2+c向上平移m个单位，所得图象的函数表达式是
     
    ；向下平移m个单位，所得图象的函数表达式是
     
    ；向左平移n个单位，所得图象的函数表达式是
     
    ；向右平移n个单位，所得图象的函数表达式是
     
    ，
    我们来研究二次函数的图象的翻折，在一张纸上作出二次函数y=x2-2x-3的图象，
    ⑤沿x轴把这张纸对折，所得图象的函数表达式是
     
    ；
    ⑥沿y轴把这张纸对折，所得图象的函数表达式是
     
    ．
    由此可以归纳二次函数y=ax2+bx+c若沿x轴翻折，所得图象的函数表达式是
     
    ，若沿y轴翻折，所得图象的函数表达式是
     
    ．
    我们继续研究二次函数的图象的旋转，将二次函数y=-
    12
    x2    +x-1的图象，绕原点旋转180°，所得图象的函数表达式是
     
    ；
    由此可以归纳二次函数y=ax2+bx+c的图象绕原点旋转180°，所得图象的函数表达式是
     
    ．（备用图如下）精英家教网
    分析：①向上平移，顶点的纵坐标1+3即可；
    ②向下平移，顶点的纵坐标1-4即可；
    ③向左平移，顶点的横坐标0-5即可；
    ④向右平移，顶点的横坐标0+6即可；
    ⑤两抛物线关于x轴对称，那么二次项的系数，一次项的系数，常数项均互为相反数；
    ⑥两抛物线关于y轴对称，二次项系数，常数项不变，一次项系数互为相反数；绕原点旋转180°可得实际是两抛物线关于x轴对称．
    解答：解：①y=2x2+4；

    ②y=2x2-3；

    ③y=2（x+5）2+1；

    ④y=2（x-6）2+1；
    y=ax2+c+m；y=ax2+c-m；y=a（x+n）2+c；y=a（x-n）2+c；

    ⑤y=-x2+2x+3；

    ⑥y=x2+2x-3 y=-ax2-bx-c；y=ax2-bx+c；y=
    1
    2
    x2-x+1；y=-ax2-bx-c．
    点评：本题考查二次函数的变化特点，需注意动手操作，观察得到相应规律．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    许多家庭以燃气作为烧水做饭的燃料，节约用气是我们日常生活中非常现实的问题．某款燃气灶旋钮位置从0度到90度（如图），燃气关闭时，燃气关闭时，燃气灶旋钮的位置为0度，旋钮角度越大，燃气流量越大，燃气开到最大时，旋钮角度为90度．为测试燃气灶旋钮在不同位置上的燃气用量，在相同条件下，选择在燃气灶旋钮的5个不同位置上分别烧开一壶水（当旋钮角度太小时，其火力不能够将水烧开，故选择旋钮角度度的范围是），记录相关数据得到下表：
    旋钮角度（度） 20 50 70 80 90
    所用燃气量（升） 73 67 83 97 115
    （1）请你从所学习过的一次函数、反比例函数和二次函数中确定哪种函数能表示所用燃气量y升与旋钮角度x度的变化规律？
    （2）当旋钮角为多少时，烧开一壶水所用燃气量最少？最少是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2012•潍坊）许多家庭以燃气作为烧水做饭的燃料，节约用气是我们日常生活中非常现实的问题．某款燃气灶旋转位置从0度到90度（如图），燃气关闭时，燃气灶旋转的位置为0度，旋转角度越大，燃气流量越大，燃气开到最大时，旋转角度为90度．为测试燃气灶旋转在不同位置上的燃气用量，在相同条件下，选择燃气灶旋钮的5个不同位置上分别烧开一壶水（当旋钮角度太小时，其火力不能够将水烧开，故选择旋钮角度x度的范围是18≤x≤90），记录相关数据得到下表：
     旋钮角度（度） 20  50  70  80  90 
     所用燃气量（升）  73  67  83  97 115 
    （1）请你从所学习过的一次函数、反比例函数和二次函数中确定哪种函数能表示所用燃气量y升与旋钮角度x度的变化规律？说明确定是这种函数而不是其它函数的理由，并求出它的解析式；
    （2）当旋钮角度为多少时，烧开一壶水所用燃气量最少？最少是多少？
    （3）某家庭使用此款燃气灶，以前习惯把燃气开到最大，现采用最节省燃气的旋钮角度，每月平均能节约燃气10立方米，求该家庭以前每月的平均燃气量．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    我们学习过二次函数的图象的平移，先作出二次函数y=2x2+1的图象．
    ①向上平移3个单位，所得图象的函数表达式是________；
    ②向下平移4个单位，所得图象的函数表达式是________；
    ③向左平移5个单位，所得图象的函数表达式是________；
    ④向右平移6个单位，所得图象的函数表达式是________．
    由此可以归纳二次函数y=ax2+c向上平移m个单位，所得图象的函数表达式是________；向下平移m个单位，所得图象的函数表达式是________；向左平移n个单位，所得图象的函数表达式是________；向右平移n个单位，所得图象的函数表达式是________，
    我们来研究二次函数的图象的翻折，在一张纸上作出二次函数y=x2-2x-3的图象，
    ⑤沿x轴把这张纸对折，所得图象的函数表达式是________；
    ⑥沿y轴把这张纸对折，所得图象的函数表达式是________．
    由此可以归纳二次函数y=ax2+bx+c若沿x轴翻折，所得图象的函数表达式是________，若沿y轴翻折，所得图象的函数表达式是________．
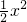    我们继续研究二次函数的图象的旋转，将二次函数y=-数学公式+x-1的图象，绕原点旋转180°，所得图象的函数表达式是________；
    由此可以归纳二次函数y=ax2+bx+c的图象绕原点旋转180°，所得图象的函数表达式是________．（备用图如下）

    查看答案和解析>>

    科目：初中数学 来源：2007年江西省中等学校招生考试数学样卷（解析版） 题型：解答题

    （2007•江西模拟）我们学习过二次函数的图象的平移，先作出二次函数y=2x2+1的图象．
    ①向上平移3个单位，所得图象的函数表达式是______；
    ②向下平移4个单位，所得图象的函数表达式是______；
    ③向左平移5个单位，所得图象的函数表达式是______；
    ④向右平移6个单位，所得图象的函数表达式是______．
    由此可以归纳二次函数y=ax2+c向上平移m个单位，所得图象的函数表达式是______；向下平移m个单位，所得图象的函数表达式是______；向左平移n个单位，所得图象的函数表达式是______；向右平移n个单位，所得图象的函数表达式是______，
    我们来研究二次函数的图象的翻折，在一张纸上作出二次函数y=x2-2x-3的图象，
    ⑤沿x轴把这张纸对折，所得图象的函数表达式是______；
    ⑥沿y轴把这张纸对折，所得图象的函数表达式是______．
    由此可以归纳二次函数y=ax2+bx+c若沿x轴翻折，所得图象的函数表达式是______，若沿y轴翻折，所得图象的函数表达式是______．
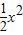    我们继续研究二次函数的图象的旋转，将二次函数y=-+x-1的图象，绕原点旋转180°，所得图象的函数表达式是______；
    由此可以归纳二次函数y=ax2+bx+c的图象绕原点旋转180°，所得图象的函数表达式是______．（备用图如下）

    查看答案和解析>>

    同步练习册答案