
【题目】如图,AC是矩形ABCD的对角线,过AC的中点O作EF⊥AC,交BC于点E,交AD于点F,连接AE,CF.
(1)求证:四边形AECF是菱形;
(2)若AB=![]() ,∠DCF=30°,求四边形AECF的面积.(结果保留根号)
,∠DCF=30°,求四边形AECF的面积.(结果保留根号)

【答案】(1)证明见解析(2)2![]()
【解析】试题分析:(1)由过AC的中点O作EF⊥AC,根据线段垂直平分线的性质,可得AF=CF,AE=CE,OA=OC,然后由四边形ABCD是矩形,易证得△AOF≌△COE,则可得AF=CE,继而证得结论;
(2)由四边形ABCD是矩形,易求得CD的长,然后利用三角函数求得CF的长,继而求得答案.
试题解析:(1)∵O是AC的中点,且EF⊥AC,
∴AF=CF,AE=CE,OA=OC,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠AFO=∠CEO,
在△AOF和△COE中,
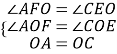
∴△AOF≌△COE(AAS),
∴AF=CE,
∴AF=CF=CE=AE,
∴四边形AECF是菱形;
(2)∵四边形ABCD是矩形,
∴CD=AB=![]() ,
,
在Rt△CDF中,cos∠DCF=![]() ,∠DCF=30°,
,∠DCF=30°,
∴CF=![]() =2,
=2,
∵四边形AECF是菱形,
∴CE=CF=2,
∴四边形AECF是的面积为:ECAB=2![]() .
.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】某旅行社为吸引市民组团去天水湾风景区旅游,推出如下收费标准:
![]() 如果人数不超过
如果人数不超过![]() 人,人均旅游费用为
人,人均旅游费用为![]() 元;
元;
![]() 如果人数超过
如果人数超过![]() 人,每增加
人,每增加![]() 人,人均旅游费用降低
人,人均旅游费用降低![]() 元,但人均旅游费用不得低于
元,但人均旅游费用不得低于![]() 元.
元.
某单位共付给该旅行社旅游费用![]() 元,问:该单位这次共有多少员工去天水湾风景区旅游?
元,问:该单位这次共有多少员工去天水湾风景区旅游?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面内有一等腰Rt△ABC,∠ACB=90°,点A在直线l上.过点C作CE⊥1于点E,过点B作BF⊥l于点F,测量得CE=3,BF=2,则AF的长为( )

A. 5 B. 4 C. 8 D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点A(0,6)的直线AB与直线OC相交于点C(2,4)动点P沿路线O→C→B运动.(1)求直线AB的解析式;(2)当△OPB的面积是△OBC的面积的![]() 时,求出这时点P的坐标;(3)是否存在点P,使△OBP是直角三角形?若存在,直接写出点P的坐标,若不存在,请说明理由.
时,求出这时点P的坐标;(3)是否存在点P,使△OBP是直角三角形?若存在,直接写出点P的坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M,N分别是正方形ABCD的边BC,CD上的点,且BM=CN, AM与BN交于点P,试探索AM与BN的关系.
(1)数量关系_____________________,并证明;
(2)位置关系_____________________,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】沐阳特产专卖店销售某种物产,其进价为每千克![]() 元,若按每千克
元,若按每千克![]() 元出售,则平均每天可售出
元出售,则平均每天可售出![]() 千克,后来经过市场调查发现,单价每降低
千克,后来经过市场调查发现,单价每降低![]() 元,平均每天的销售量增加
元,平均每天的销售量增加![]() 千克,若专卖店销售这种特产平均每天获利
千克,若专卖店销售这种特产平均每天获利![]() 元,且销量尽可能大,则每千克特产应定价为多少元?
元,且销量尽可能大,则每千克特产应定价为多少元?
![]() 解:方法
解:方法![]() :设每千克特产应降价
:设每千克特产应降价![]() 元,由题意,得方程为: ________;
元,由题意,得方程为: ________;
方法![]() :设每千克特产降价后定价为
:设每千克特产降价后定价为![]() 元,由题意,得方程为:________.
元,由题意,得方程为:________.
![]() 请你选择其中一种方法完成解答.
请你选择其中一种方法完成解答.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P为定角∠AOB的平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:(1)PM=PN恒成立;(2)OM+ON的值不变;(3)四边形PMON的面积不变;(4)MN的长不变,其中正确的个数为( )

A. 4B. 3C. 2D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知函数y=x+1的图象与y轴交于点A,一次函数y=kx+b的图象经过点B(0,﹣1),与x轴以及y=x+1的图象分别交于点C、D,且点D的坐标为(1,n),
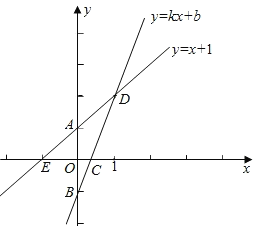
(1)求一次函数y=kx+b的函数关系式
(2)求四边形AOCD的面积;
(3)是否存在y轴上的点P,使得以BD为底的△PBD等腰三角形?若存在求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,射线AP在△ABC的外侧,点B关于AP的对称点为D,连接CD交射线AP于点E,连接BE.
(1)根据题意补全图形;
(2)求证:CD=EB+EC;
(3)求证:∠ABE=∠ACE.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com