
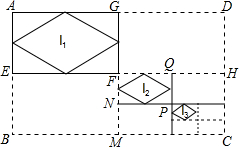
 如图,在矩形ABCD中,AD=a,AB=b,连接其对边中点,得到四个矩形,顺次连接矩形AEFG各边中点,得到菱形I1;连接矩形FMCH对边中点,又得到四个矩形,顺次连接矩形FNPQ各边中点,得到菱形I2;…如此操作下去,得到菱形I2016,则I2016的面积是($\frac{1}{2}$)4033ab.
如图,在矩形ABCD中,AD=a,AB=b,连接其对边中点,得到四个矩形,顺次连接矩形AEFG各边中点,得到菱形I1;连接矩形FMCH对边中点,又得到四个矩形,顺次连接矩形FNPQ各边中点,得到菱形I2;…如此操作下去,得到菱形I2016,则I2016的面积是($\frac{1}{2}$)4033ab. 分析 利用菱形的面积为两对角线乘积的一半,得到菱形I1 的面积,同理可得菱形I2的面积,根据规律可得菱形I2016的面积.
解答 解:由题意得:菱形I1 的面积为:$\frac{1}{2}$×AG×AE=$\frac{1}{2}$×$\frac{1}{2}$a×$\frac{1}{2}$b=($\frac{1}{2}$)3•ab;
菱形I2的面积为:$\frac{1}{2}$×FQ×FN=$\frac{1}{2}$×($\frac{1}{2}$×$\frac{1}{2}$a)×($\frac{1}{2}$×$\frac{1}{2}$b)=($\frac{1}{2}$)5•ab;
…,
∴菱形In的面积为:($\frac{1}{2}$)2n+1ab,
故I2016的面积是:($\frac{1}{2}$)2×2016+1ab=($\frac{1}{2}$)4033ab.
故答案为:($\frac{1}{2}$)4033ab.
点评 本题主要考查了菱形面积的计算和规律的归纳,利用菱形的面积为两对角线乘积的一半,是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
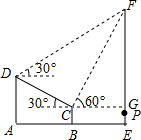 如图是某校体育场内一看台的截面图,看台CD与水平线的夹角为30°,最低处C与地面的距离BC为2.5米,在C,D正前方有垂直于地面的旗杆EF,在C,D两处测得旗杆顶端F的仰角分别为60°和30°,CD长为10米,升旗仪式中,当国歌开始播放时,国旗也在离地面1.5米的P处同时冉冉升起,国歌播放结束时,国旗刚好上升到旗杆顶端F,已知国歌播放时间为46秒,求国旗上升的平均速度.(结果精确到0.01米/秒)
如图是某校体育场内一看台的截面图,看台CD与水平线的夹角为30°,最低处C与地面的距离BC为2.5米,在C,D正前方有垂直于地面的旗杆EF,在C,D两处测得旗杆顶端F的仰角分别为60°和30°,CD长为10米,升旗仪式中,当国歌开始播放时,国旗也在离地面1.5米的P处同时冉冉升起,国歌播放结束时,国旗刚好上升到旗杆顶端F,已知国歌播放时间为46秒,求国旗上升的平均速度.(结果精确到0.01米/秒)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com