
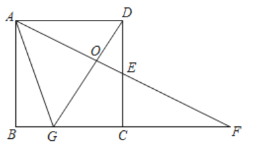
【题目】如图,在矩形![]() 中,
中,![]() ,点
,点![]() 是边
是边![]() 的中点,
的中点,![]() 和
和![]() 的延长线交于点
的延长线交于点![]() ,点
,点![]() 是边
是边![]() 上的一点,且满足
上的一点,且满足![]() ,连接
,连接![]() ,
,![]() ,且
,且![]() 与
与![]() 交于点
交于点![]() .
.
(1)若![]() ,求
,求![]() 的面积
的面积
(2)当![]() 是直角三角形时,求所有满足要求的
是直角三角形时,求所有满足要求的![]() 值.
值.
(3)记![]() ,
,![]() ,
,
①求![]() 关于
关于![]() 的函数关系.
的函数关系.
②当![]() 时,求
时,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)①
;(3)①![]() ;②
;②![]()
【解析】
(1)当a=1时,CG=1,BC=3,GC=2,先由矩形的性质及已知证得![]() ,求出CF=AD=BC=3,再证得
,求出CF=AD=BC=3,再证得![]() 得
得![]() ,然后由等高的面积比等于相似比求得
,然后由等高的面积比等于相似比求得![]() 的面积;
的面积;
(2)分两种情况:①![]() ,②
,②![]() ,利用相似三角形的判定与性质求解即可;
,利用相似三角形的判定与性质求解即可;
(3)①由![]() 和
和![]() 可证得
可证得![]() ,根据同底的三角形面积比等于相似比即可求解
,根据同底的三角形面积比等于相似比即可求解![]() 关于
关于![]() 的函数关系;
的函数关系;
②由已知证得![]() ,得到
,得到 ,过O作OH⊥AD于H,由勾股定理得关于a的方程,解之得到AD,即可求得
,过O作OH⊥AD于H,由勾股定理得关于a的方程,解之得到AD,即可求得![]() .
.
(1)当a=1时,CG=1,BC=3,GC=2,
![]() 矩形
矩形![]() 中,
中,![]() ,
,
![]() ,AD=BC=3,
,AD=BC=3,
又![]() ,
,
![]() ,
,
![]() ,
,
∴CF=AD=3,
![]() ,
,
∵![]() ,
,![]()
∴![]() ,
,
![]() ,
,
∵ΔAOG底边OG上的高与ΔAGD底边GD的高相等,
![]()
(2)![]()
![]() 分两种情形讨论
分两种情形讨论
情形①:如图1,![]() ,
,
∵![]()
∴![]() ,又AB=8,
,又AB=8,
![]() ,
,![]()
易证![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
易证![]() ,
,![]()
∴![]()
![]()
![]()
![]()

情形②:如图2,![]() ,
,
∵∠AGB+∠BAG=90,∠AGB+∠DGC=90,
∴∠BAG=∠DGC,
![]()
![]()
![]()
![]()

(3)①∵![]() ,
,
∴![]() ,
,
又![]()
∴AE=EF,
![]()
![]()
又![]()
![]() ,
,
②![]() ,
,![]()
![]()
 ,即
,即![]() ,
,
过O作OH⊥AD于H,则有
![]() ,
,

![]() ,
,
∴AD=BC=12,
![]() .
.



 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
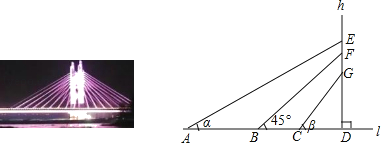
【题目】如图,是一座横跨沙颖河的斜拉桥,拉索两端分别固定在主梁l和索塔h上,索塔h垂直于主梁l,垂足为D.拉索AE,BF,CG的仰角分别是α,45°,β,且α+β=90°(α<β),AB=15m,BC=5m,CD=4m,EF=3FG,求拉索AE的长.(精确到1m,参考数据:![]() ≈2.24,
≈2.24,![]() ≈1.41)
≈1.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
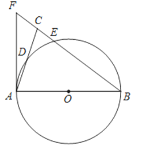
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于点D,E,BC的延长线与⊙O的切线AF交于点F.
(1)求证:∠ABC=2∠CAF;
(2)若AC=2![]() ,CE:EB=1:4,求CE,AF的长.
,CE:EB=1:4,求CE,AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
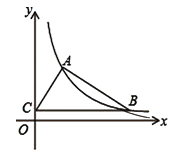
【题目】已知:如图,第一象限内的点A,B在反比例函数的图象上,点C在y轴上,BC∥x轴,点A的坐标为(2,4),且tan∠ACB=![]()
求:(1)反比例函数的解析式;
(2)点C的坐标;
(3)∠ABC的余弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
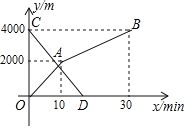
【题目】小玲和弟弟小东分别从家和图书馆同时出发,沿同一条路相向而行,小玲开始跑步中途改为步行,到达图书馆恰好用30min.小东骑自行车以300m/min的速度直接回家,两人离家的路程y(m)与各自离开出发地的时间x(min)之间的函数图象如图所示
(1)家与图书馆之间的路程为多少m,小玲步行的速度为多少m/min;
(2)求小东离家的路程y关于x的函数解析式,并写出自变量的取值范围;
(3)求两人相遇的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
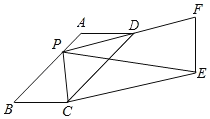
【题目】如图,已知平行四边形ABCD中,∠B=60°,AB=12,BC=5,P为AB上任意一点(可以与A、B重合),延长PD到F,使得DF=PD,以PF、PC为边作平行四边形PCEF,则PE长度的最小值____.
查看答案和解析>>
科目:初中数学 来源: 题型:
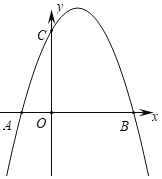
【题目】如图,抛物线L1:y=ax2+bx+c(a≠0)与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0),OB=OC=3OA.若抛物线L2与抛物线L1关于直线x=2对称.
(1)求抛物线L1与抛物线L2的解析式;
(2)在抛物线L1上是否存在一点P,在抛物线L2上是否存在一点Q,使得以BC为边,且以B、C、P、Q为顶点的四边形为平行四边形?若存在,求出P、Q两点的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
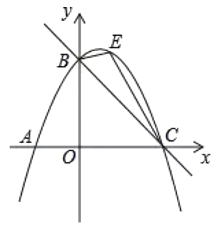
【题目】如图,直线![]() 与 x 轴交于点 C,与 y 轴交于点 B,抛物线
与 x 轴交于点 C,与 y 轴交于点 B,抛物线 ![]() 经过 B、C 两点.
经过 B、C 两点.
(1)求抛物线的解析式;
(2)如图,点 E 是抛物线上的一动点(不与 B,C 两点重合),△BEC 面积记为 S,当 S 取何值时,对应的点 E 有且只有三个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com