
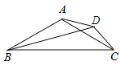
【题目】如图:等腰△ABC中,AB=AC,点D在AC右侧,∠BAC=∠BDC=120°
(1)猜想DA,DC,DB的数量关系并证明
(2)点D 在AB边左侧时三条线段关系是否发生变化?请画出图形。若变化,直接写出结论.
【答案】(1)DB=DC+![]() AD,理由见解析;
AD,理由见解析;
(2)CD=BD +![]() AD,理由见解析.
AD,理由见解析.
【解析】
(1)在BD上取点E使AE=AD,作AF⊥ED,根据等腰三角形的性质得到EF=FD,根据三角形内角和定理得到∠ABC=∠ACB=30°,根据圆周角定理得到∠ADE=∠ACB=30°,根据勾股定理得到DF=![]() AD,证明△BAE≌△CAD,根据全等三角形的性质得到BE=CD,结合图形证明即可;
AD,证明△BAE≌△CAD,根据全等三角形的性质得到BE=CD,结合图形证明即可;
(2)结论:CD=![]() AD+BD.在CD上取点M使AM=AD,作AN⊥DM,根据等腰三角形的性质得到DN=MN,根据三角形内角和定理得到∠ABC=∠ACB=30°,根据圆周角定理得到∠ADC=∠ABC=30°,根据勾股定理得到DN=
AD+BD.在CD上取点M使AM=AD,作AN⊥DM,根据等腰三角形的性质得到DN=MN,根据三角形内角和定理得到∠ABC=∠ACB=30°,根据圆周角定理得到∠ADC=∠ABC=30°,根据勾股定理得到DN=![]() AD,证明△DAB≌△MAC,根据全等三角形的性质得到BD=CM,结合图形证明即可.
AD,证明△DAB≌△MAC,根据全等三角形的性质得到BD=CM,结合图形证明即可.
(1)DB=DC+![]() AD,
AD,
理由如下:在BD上取点E使AE=AD,作AF⊥ED,则EF=FD,
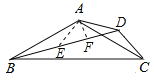
∵AB=AC,∠BAC=120°,
∴∠ABC=∠ACB=30°,
∵∠BAC=∠BDC=120°,
∴A,B,C,D四点共圆,
∴∠ADB=∠ACB=30°,
∴AF=![]() AD,
AD,
∴DF=![]() AD,
AD,
∴DE=![]() AD,
AD,
∵∠BAC=120°,∠EAD=120°,
∴∠BAE=∠CAD,
在△BAE和△CAD中,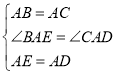 ,
,
∴△BAE≌△CAD(SAS)
∴BE=CD,
∴DB=BE+DE=DC+![]() AD;
AD;
(2)如图:
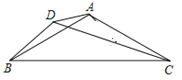
CD=BD +![]() AD,
AD,
理由:在CD上取点M使AM=AD,作AN⊥DM,则DN=MN,

∵AB=AC,∠BAC=120°,
∴∠ABC=∠ACB=30°,
∵∠BAC=∠BDC=120°,
∴A,B,C,D四点共圆,
∴∠ADC=∠ABC=30°,
∴AN=![]() AD,
AD,
∴DN=![]() AD,
AD,
∴DM=![]() AD,
AD,
∵∠DAM=120°,∠BAC=120°,
∴∠DAB=∠MAC,
在△DAB和△MAC中,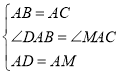 ,
,
∴△DAB≌△MAC(SAS)
∴BD=CM,
∴DC=CM+DM=BD+![]() AD.
AD.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案科目:初中数学 来源: 题型:
【题目】下列说法:①若直线PE是线段AB的垂直平分线,则![]() ,
,![]() ;②若
;②若![]() ,
,![]() ,则直线PE是线段AB的垂直平分线;③若
,则直线PE是线段AB的垂直平分线;③若![]() ,
,![]() ,则AB垂直平分PE;④若
,则AB垂直平分PE;④若![]() ,则点P必是线段AB的垂直平分线上的点;⑤若
,则点P必是线段AB的垂直平分线上的点;⑤若![]() ,则过点E的直线垂直平分线段AB.其中正确的个数有( ).
,则过点E的直线垂直平分线段AB.其中正确的个数有( ).
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 “赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
请结合图表完成下列各题:
(1)①表中a的值为 ,中位数在第 组;
②频数分布直方图补充完整;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
(3)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.
组别 | 成绩x分 | 频数(人数) |
第1组 | 50≤x<60 | 6 |
第2组 | 60≤x<70 | 8 |
第3组 | 70≤x<80 | 14 |
第4组 | 80≤x<90 | a |
第5组 | 90≤x<100 | 10 |

查看答案和解析>>
科目:初中数学 来源: 题型:
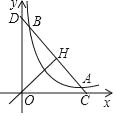
【题目】如图,已知直线y=﹣x+b(b>0)与其垂线y=x交于H,与双曲线c:y=![]() (k>0)在第一象限交于A,B,与两坐标轴交于C,D.
(k>0)在第一象限交于A,B,与两坐标轴交于C,D.
(1)当A的坐标为(2,1)时,求k的值和OH的长;
(2)若CH2﹣HA2=4,求双曲线c的方程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴分别交于点A、B,与y轴交于点C,且OA=1,OB=3,顶点为D,对称轴交x轴于点Q.

(1)求抛物线对应的二次函数的表达式;
(2)点P是抛物线的对称轴上一点,以点P为圆心的圆经过A、B两点,且与直线CD相切,求点P的坐标;
(3)在抛物线的对称轴上是否存在一点M,使得△DCM∽△BQC?如果存在,求出点M的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A、B分别在x轴、y轴上.
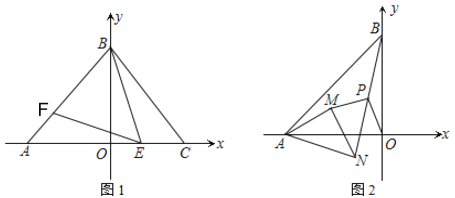
(1)如图1,点A与点C关于y轴对称,点E、F分别是线段AC、AB上的点(点E不与点A、C重合),且∠BEF=∠BAO.若∠BAO=2∠OBE,求证:AF=CE;
(2)如图2,若OA=OB,在点A处有一等腰△AMN绕点A旋转,且AM=MN,∠AMN=90°.连接BN,点P为BN的中点,试猜想OP和MP的数量关系和位置关系,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
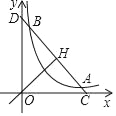
【题目】如图,已知直线y=﹣x+b(b>0)与其垂线y=x交于H,与双曲线c:y=![]() (k>0)在第一象限交于A,B,与两坐标轴交于C,D.
(k>0)在第一象限交于A,B,与两坐标轴交于C,D.
(1)当A的坐标为(2,1)时,求k的值和OH的长;
(2)若CH2﹣HA2=4,求双曲线c的方程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店准备购进甲、乙两种服装出售,甲种每件售价120元,乙种每件售价90元.每件甲服装的进价比乙服装的进价贵20元,购进3件甲服装的费用和购进4件乙服装的费用相等,现计划购进两种服装共100件,其中甲种服装不少于65件.
(1)甲种服装进价为 元/件,乙种服装进价为 元/件;
(2)若购进这100件服装的费用不得超过7500元.
①求甲种服装最多购进多少件?
②该服装店对甲种服装每件降价![]() 元,乙种服装价格不变,如果这100件服装都可售完,那么该服装店如何进货才能获得最大利润?
元,乙种服装价格不变,如果这100件服装都可售完,那么该服装店如何进货才能获得最大利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在综合与实践课上,老师组织同学们以“矩形纸片的折叠”为主题开展数学活动.
(1)奋进小组用图1中的矩形纸片ABCD,按照如图2所示的方式,将矩形纸片沿对角线AC折叠,使点B落在点![]() 处,则
处,则![]() 与
与![]() 重合部分的三角形的类型是________.
重合部分的三角形的类型是________.
(2)勤学小组将图2中的纸片展平,再次折叠,如图3,使点A与点C重合,折痕为EF,然后展平,则以点A、F、C、E为顶点的四边形是什么特殊四边形?请说明理由.
(3)创新小组用图4中的矩形纸片ABCD进行操作,其中![]() ,
,![]() ,先沿对角线BD对折,点C落在点
,先沿对角线BD对折,点C落在点![]() 的位置,
的位置,![]() 交AD于点G,再按照如图5所示的方式折叠一次,使点D与点A重合,得折痕EN,EN交AD于点M.则EM的长为________cm.
交AD于点G,再按照如图5所示的方式折叠一次,使点D与点A重合,得折痕EN,EN交AD于点M.则EM的长为________cm.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com