

���� ��1����ͼ1�У���AM��BC��M����IH��N���������α߳�Ϊx����IH��BC����$\frac{AN}{AM}$=$\frac{IH}{BC}$�г����̼��ɽ�����⣮
��2������λ��֪ʶ���ҵ�Բ��M���ɽ�����⣮
��� �⣺��1����ͼ1�У���AM��BC��M����IH��N���������α߳�Ϊx��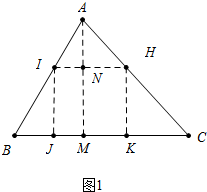
��RT��ABM�У��ߡ�AMB=90�㣬��B=60�㣬AB=4��
��BM=2��AM=2$\sqrt{3}$��
�ߡ�C=��MAC=45�㣬
��AM=MC=2$\sqrt{3}$��
��BC=2+2$\sqrt{3}$
��IH��BC��
��$\frac{AN}{AM}$=$\frac{IH}{BC}$��
��$\frac{2\sqrt{3}-x}{2\sqrt{3}}$=$\frac{x}{2+2\sqrt{3}}$��
��x=$\frac{6+10\sqrt{3}}{11}$
��С��������������������εı߳�Ϊ$\frac{6+10\sqrt{3}}{11}$��
��2����ͼ2�У�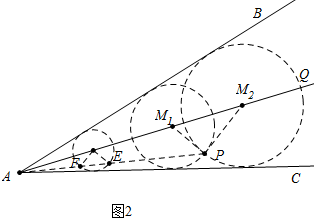
������BAC��ƽ����AQ��
����AQ��ȡһ��O������O��AB��AC���У�
������AP����O��E��F��
����PM1��OE��AQ��M1��
����M1ΪԲ��PM1Ϊ�뾶����M1��
��M1������
ͬ������PM2��OF����AQ��M2��
��M2������
���� ���⿼��λ�Ʊ任�������ε����ʡ����������ε����ʵ�֪ʶ������Ĺؼ������Ӧ����Щ֪ʶ������⣬�����п��������ͣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 700 | B�� | 10% | C�� | 70 | D�� | 7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ�٣���֪��ABC�ǵ��������Σ���BAC=90�㣬��D��BC���е㣬��������DEFG��ʹ��A��C�ֱ���DG��DE�ϣ�����AE��BG��
��ͼ�٣���֪��ABC�ǵ��������Σ���BAC=90�㣬��D��BC���е㣬��������DEFG��ʹ��A��C�ֱ���DG��DE�ϣ�����AE��BG���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ����x�����棩 | �� | 0 | 5 | 10 | 15 | �� |
| ����y����m/s�� | �� | 331 | 334 | 337 | 340 | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪������l1����ԭ����A�㣬�䶥����P��-2��3����ƽ����y���ֱ��m��x�ύ�ڵ�B��b��0������������l1���ڵ�M��
��ͼ����֪������l1����ԭ����A�㣬�䶥����P��-2��3����ƽ����y���ֱ��m��x�ύ�ڵ�B��b��0������������l1���ڵ�M���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com