
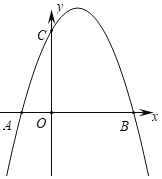
【题目】如图,抛物线L1:y=ax2+bx+c(a≠0)与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0),OB=OC=3OA.若抛物线L2与抛物线L1关于直线x=2对称.
(1)求抛物线L1与抛物线L2的解析式;
(2)在抛物线L1上是否存在一点P,在抛物线L2上是否存在一点Q,使得以BC为边,且以B、C、P、Q为顶点的四边形为平行四边形?若存在,求出P、Q两点的坐标,若不存在,请说明理由.
【答案】(1)抛物线L1的解析式为y=-x2+2x+3,抛物线L2的解析式为y=-(x-3)2+4;(2)存在P(2,3),Q(5,0)或P(![]() ,
,![]() ),Q(
),Q(![]() ,
,![]() ),使得以BC为边且以B、C、P、Q为顶点的四边形为平行四边形.
),使得以BC为边且以B、C、P、Q为顶点的四边形为平行四边形.
【解析】
(1)用待定系数法求抛物线L1的解析式并配方成顶点式,得到抛物线L1的顶点坐标D;由抛物线L2与抛物线L1关于直线x=2对称可得两抛物线开口方向、大小相同,且两顶点关于直线x=2对称,因此求得抛物线L2的顶点D',进而得到抛物线L2的顶点式;
(2)由于BC为边,以B、C、P、Q为顶点的四边形为平行四边形,所以有两种情况:①BQ∥PC,BQ=PC;②BP∥CQ,BP=CQ.因为可把点B、C之间看作是向左(或右)平移3个单位,再向上(或下)平移3个单位得到,所以点P、Q之间也有相应的平移关系,故可由点P坐标(t,t+2t+3)的t表示点Q坐标,再把点Q坐标代入抛物线L2解方程即求得t的值,进而求得点P、Q坐标.
(1)∵A(﹣1,0),
∴OB=OC=3OA=3,
∴B(3,0),C(0,3)
∵抛物线L1:y=ax2+bx+c经过点A、B、C,
∴ ,解得:
,解得: ,
,
∴抛物线L1的解析式为y=-x2+2x+3=-(x-1)2+4,
∴抛物线L1的顶点D(1,4),
∵抛物线L2与抛物线L1关于直线x=2对称,
∴两抛物线开口方向、大小相同,抛物线L2的顶点D'与点D关于直线x=2对称,
∴D'(3,4),
∴抛物线L2的解析式为y=-(x-3)2+4;
(2)存在满足条件的P、Q,使得以BC为边且以B、C、P、Q为顶点的四边形为平行四边形,设抛物线L1上的P(t,-t2+2t+3),
①若四边形BCPQ为平行四边形,如图1,

∴BQ∥PC,BQ=PC,
∴BQ可看作是CP向右平移3个单位,再向下平移3个单位得到的,
∴Q(t+3,-t2+2t),
∵点Q在抛物线L2上,
∴﹣t2+2t=-(t+3-3)2+4,解得:t=2,
∴P(2,3),Q(5,0);
②若四边形BCQP为平行四边形,如图2,
∴
BP∥CQ,BP=CQ,
∴CQ可看作是BP向左平移3个单位,再向上平移3个单位得到的,
∴Q(t﹣3,-t2+2t+6),
∴﹣t2+2t+6=-(t-3-3)2+4,解得:t![]() ,
,
∴P(![]() ,
,![]() ),Q(
),Q(![]() ,
,![]() );
);
综上所述:存在P(2,3),Q(5,0)或P(![]() ,
,![]() ),Q(
),Q(![]() ,
,![]() ),使得以BC为边且以B、C、P、Q为顶点的四边形为平行四边形.
),使得以BC为边且以B、C、P、Q为顶点的四边形为平行四边形.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC=6,E,F分别是AB,AC的中点,动点P在射线EF上,BP交CE于点D,∠CBP的平分线交CE于点Q,当CQ=![]() CE时,EP+BP的值为( )
CE时,EP+BP的值为( )
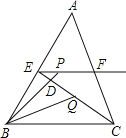
A.6B.9C.12D.18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“只要人人都献出一点爱,世界将变成美好的人间”,在新型肺炎疫情期间,全国人民万众一心,众志成城,共克时艰.某社区积极发起“援鄂捐款”活动倡议,有2500名居民踊跃参与献爱心.社区管理员随机抽查了部分居民捐款情况,统计图如图:
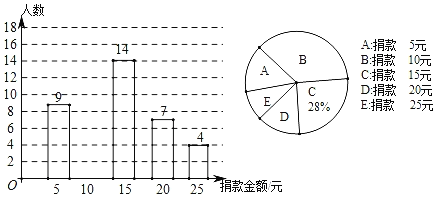
(1)计算本次共抽查居民人数,并将条形图补充完整;
(2)根据统计情况,请估计该社区捐款20元以上(含20元)的居民有多少人?
(3)该社区有1名男管理员和3名女管理员,现要从中随机挑选2名管理员参与“社区防控”宣讲活动,请用列表法或树状图法求出恰好选到“1男1女”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,点
,点![]() 是边
是边![]() 的中点,
的中点,![]() 和
和![]() 的延长线交于点
的延长线交于点![]() ,点
,点![]() 是边
是边![]() 上的一点,且满足
上的一点,且满足![]() ,连接
,连接![]() ,
,![]() ,且
,且![]() 与
与![]() 交于点
交于点![]() .
.
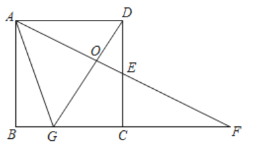
(1)若![]() ,求
,求![]() 的面积
的面积
(2)当![]() 是直角三角形时,求所有满足要求的
是直角三角形时,求所有满足要求的![]() 值.
值.
(3)记![]() ,
,![]() ,
,
①求![]() 关于
关于![]() 的函数关系.
的函数关系.
②当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某种电动汽车的性能,对这种电动汽车进行了抽检,将一次充电后行驶的里程数分为A,B,C,D四个等级,其中相应等级的里程依次为200千米,210千米,220千米,230千米,获得如下不完整的统计图,根据信息解答下列问题:

(1)问这次被抽检的电动汽车共有几辆?并补全条形统计图:
(2)求电动汽车一次充电后行驶里程数的中位数、众数:
(3)一次充电后行驶里程数220千米以上(含220千米)为优质等级,若全市有这种电动汽车1200辆,估计优质等级的电动汽车约为多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刚从家出发匀速步行去学校上学.几分钟后发现忘带数学作业,于是掉头原速返回并立即打电话给爸爸,挂断电话后爸爸立即匀速跑步去追小刚,同时小刚以原速的两倍匀速跑步回家,爸爸追上小刚后以原速的![]() 倍原路步行回家.由于时间关系小明拿到作业后同样以之前跑步的速度赶往学校,并在从家出发后23分钟到校(小刚被爸爸追上时交流时间忽略不计).两人之间相距的路程y(米)与小刚从家出发到学校的步行时间x(分钟)之间的函数关系如图所示,则小刚家到学校的路程为_____米.
倍原路步行回家.由于时间关系小明拿到作业后同样以之前跑步的速度赶往学校,并在从家出发后23分钟到校(小刚被爸爸追上时交流时间忽略不计).两人之间相距的路程y(米)与小刚从家出发到学校的步行时间x(分钟)之间的函数关系如图所示,则小刚家到学校的路程为_____米.
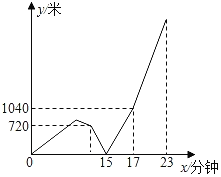
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于反比例函数![]() ,下列说法不正确的是( )
,下列说法不正确的是( )
A. 函数图象分别位于第一、第三象限
B. 当x>0时,y随x的增大而减小
C. 若点A(x1,y1),B(x2,y2)都在函数图象上,且x1<x2,则y1>y2
D. 函数图象经过点(1,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为等边
为等边![]() 的高,
的高,![]() ,点P为直线
,点P为直线![]() 上的动点(不与点B重合),连接
上的动点(不与点B重合),连接![]() ,将线段
,将线段![]() 绕点P逆时针旋转60°,得到线段
绕点P逆时针旋转60°,得到线段![]() ,连接
,连接![]() 、
、![]() .
.
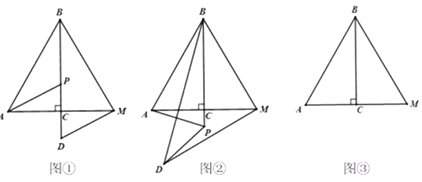
(1)问题发现:如图①,当点D在直线![]() 上时,线段
上时,线段![]() 与
与![]() 的数量关系为_________,
的数量关系为_________,![]() _________;
_________;
(2)拓展探究:如图②,当点P在![]() 的延长线上时,(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由;
的延长线上时,(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由;
(3)问题解决:当![]() 时,请直接写出线段
时,请直接写出线段![]() 的长度.
的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com