
【题目】如图,已知平行四边形OABC的三个顶点A、B、C在以O为圆心的半圆上,过点C作CD⊥AB,分别交AB、AO的延长线于点D、E,AE交半圆O于点F,连接CF. 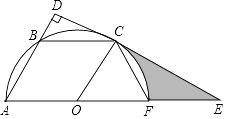
(1)判断直线DE与半圆O的位置关系,并说明理由;
(2)①求证:CF=OC; ②若半圆O的半径为12,求阴影部分的周长.
【答案】
(1)解:结论:DE是⊙O的切线.
理由:∵四边形OABC是平行四边形,
又∵OA=OC,
∴四边形OABC是菱形,
∴OA=OB=AB=OC=BC,
∴△ABO,△BCO都是等边三角形,
∴∠AOB=∠BOC=∠COF=60°,
∵OB=OF,
∴OG⊥BF,
∵AF是直径,CD⊥AD,
∴∠ABF=∠DBG=∠D=∠BGC=90°,
∴四边形BDCG是矩形,
∴∠OCD=90°,
∴DE是⊙O的切线.

(2)①证明由(1)可知:∠COF=60°,OC=OF,
∴△OCF是等边三角形,
∴CF=OC.
②解:在Rt△OCE中,∵OC=12,∠COE=60°,∠OCE=90°,
∴OE=2OC=24,EC=12 ![]() ,
,
∵OF=12,
∴EF=12,
∴ ![]() 的长=
的长= ![]() =4π,
=4π,
∴阴影部分的周长为4π+12+12 ![]() .
.
【解析】(1)结论:DE是⊙O的切线.首先证明△ABO,△BCO都是等边三角形,再证明四边形BDCG是矩形,即可解决问题;(2)①只要证明△OCF是等边三角形即可解决问题;②求出EC、EF、弧长CF即可解决问题.


科目:初中数学 来源: 题型:
【题目】某小组做“用频率估计概率”的试验时,统计了某一事件发生的频率,绘制了如图所示的折线图. 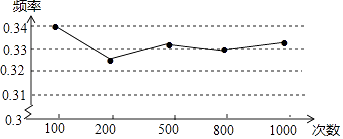
该事件最有可能是(填写一个你认为正确的序号).
①掷一个质地均匀的正六面体骰子,向上一面的点数是2;
②掷一枚硬币,正面朝上;
③暗箱中有1个红球和2个黄球,这些球除了颜色外无其他差别,从中任取一球是红球.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读以下内容:
已知实数x,y满足x+y=2,且![]() 求k的值.
求k的值.
三位同学分别提出了以下三种不同的解题思路:
甲同学:先解关于x,y的方程组![]() ,再求k的值.
,再求k的值.
乙同学:先将方程组中的两个方程相加,再求k的值.
丙同学:先解方程组![]() ,再求k的值.
,再求k的值.
(2)你最欣赏(1)中的哪种思路?先根据你所选的思路解答此题,再对你选择的思路进行简要评价.
(评价参考建议:基于观察到题目的什么特征设计的相应思路,如何操作才能实现这些思路、运算的简洁性,以及你依此可以总结什么解题策略等等)
请先在以下相应方框内打勾,再解答相应题目.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E. 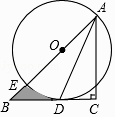
(1)求证:AD平分∠BAC;
(2)若CD=1,求图中阴影部分的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC = 90°,BC = 1,AC =![]() .
.

(1)以点B为旋转中心,将△ABC沿逆时针方向旋转90°得到△A′BC′,请画出变换后的图形;
(2)求点A和点A′之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B两地相距200km,一列火车从B地出发沿BC方向以![]() 的速度行驶,在行驶过程中,这列火车离A地的路程
的速度行驶,在行驶过程中,这列火车离A地的路程![]() 与行驶时间
与行驶时间![]() 之间的函数关系式是______.
之间的函数关系式是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校兴趣小组对网上吐糟较为频繁的“医患关系”产生了兴趣,利用节假日在某社区开展了“造成医患关系紧张的原因”的问卷调查.
造成医患关系紧张的原因(单选) |
根据调查结果绘制出了如下两幅尚不完整的统计图.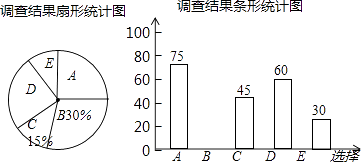
根据以上信息解答下列问题:
(1)这次接受调查的总人数为人;
(2)在扇形统计图中,“A”所在扇形的圆心角的度数为;
(3)补全条形统计图;
(4)若该市有1000万人,请你估计选D的总人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com