
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪������y=ax2+bx-8��x�ύ��A��B���㣬��y�ύ�ڵ�C��ֱ��l��������ԭ��O���������ߵ�һ������ΪD���������ߵĶԳ��ύ�ڵ�E������CE����֪��A��D������ֱ�Ϊ��-2��0������6��-8����
��1���������ߵĺ�������ʽ�����ֱ������B�͵�E�����ꣻ
��2������P��y�Ḻ�����ϵ�һ�����㣬��������Ϊ��0��m����ֱ��PB��ֱ��l���ڵ�Q����̽������mΪ��ֵʱ����OPQ�ǵ��������Σ�
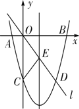
���𰸡�(1)y��![]() x2��3x��8��B(8��0),E(3����4)��(2)m��ֵΪ��
x2��3x��8��B(8��0),E(3����4)��(2)m��ֵΪ��![]() ��
��![]() .
.
��������
��1�����ݴ���ϵ������������߽���ʽ���������B���꣬���ֱ��OD����ʽ���ɽ����E������
��2������ͼ1�У���OP=OQʱ����OPQ�ǵ��������Σ�����E��ֱ��ME��PB����y���ڵ�M����x���ڵ�H�������M��H�����꼴�ɽ�����⣮����ͼ2�У���QO=QPʱ����POQ�ǵ��������Σ���֤��CE��PQ������ƽ���ߵ������г����̼��ɽ�����⣮
��1����������y��ax2��bx��8������A(��2��0)��D(6����8)��
�ཫA��D�������������![]() ��
��
���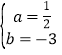 ��
��
�������ߵĺ�������ʽΪy��![]() x2��3x��8��
x2��3x��8��
��2�������������������ۣ�
�ٵ�OP��OQʱ����OPQ�ǵ��������Σ����ͼ����
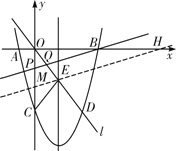
ͼ1
�ߵ�E������Ϊ(3����4)��
��OE��![]() ��5��
��5��
����E��ֱ��ME��PB����y���ڵ�M����x���ڵ�H��
��![]() ��
��![]() ��
��
��OM��OE��5��
���M������Ϊ(0����5)��
��ֱ��ME�ĺ�������ʽΪy��k1x��5��E��3��-4����ֱ��ME�ϣ�
��3k1��5����4�����k1��![]() ��
��
��ֱ��ME�ĺ�������ʽΪy��![]() x��5��
x��5��
��y��0�����x��15��
���H������Ϊ(15��0)��
�֡�MH��PB��
��![]() ��
��![]() ����
����![]() ��
��
��m����![]() ��
��
�ڵ�QO��QPʱ����OPQ�ǵ��������Σ���ͼ��
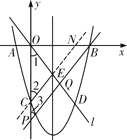
�ߵ�x��0ʱ��y��![]() x2��3x��8����8��
x2��3x��8����8��
���C������Ϊ(0����8)��
��CE��![]() ��5��
��5��
��OE��CE��
���1����2��
�֡�QO��QP��
���1����3��
���2����3��
��CE��PB.
��ֱ��CE��x���ڵ�N���亯������ʽΪy��k2x��8��
E��3��-4����ֱ��CE�ϣ�
��3k2��8����4�����k2��![]() ��
��
��ֱ��CE�ĺ�������ʽΪy��![]() x��8��
x��8��
��y��0����![]() x��8��0��
x��8��0��
��x��6��
���N������Ϊ(6��0)��
��CN��PB.
��![]() ��
��![]() ��
��
��![]() ��
��![]() �����m����
�����m����![]() .
.
������������m��ֵΪ��![]() ��
��![]() ʱ����OPQ�ǵ��������Σ�
ʱ����OPQ�ǵ��������Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ֽ��ÿ��С�����εı߳����ǵ�λ1����OAB��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ��������⣺
��1���밴Ҫ�����ABO�����±任��
������OAB����ƽ��2����λ��������ƽ��3����λ�õ���O1A1B1��
���Ե�OΪλ�����ģ�λ�Ʊ�Ϊ2��1������ABC��λ�����ĵ������зŴ�õ���OA2B2��
��2��д����A1��A2�����꣺ �� ��
��3����OA2B2�����Ϊ ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
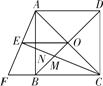
����Ŀ����ͼ��������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O���ӳ�CB����F��ʹCF��CA������AF����ACF��ƽ���߷ֱ�AF��AB��BD�ڵ�E��N��M������EO.
(1)��֪EO��![]() ����������ABCD�ı߳���
����������ABCD�ı߳���
(2)�����߶�EM��CN��������ϵ������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳���A��B������Ʒ������2��A��Ʒ��1��B��Ʒ������80Ԫ������3��A��Ʒ��2��B��Ʒ������135Ԫ��
��1����A��B������Ʒÿ���ۼ۷ֱ�ΪaԪ��bԪ����a��b��ֵ��
��2��B��Ʒÿ���ijɱ���20Ԫ�������г����飺������1��������ĵ������ۣ����̳�ÿ������B��Ʒ100���������۵���ÿ����1Ԫ��B��Ʒÿ����������ͼ���5����
����ÿ��B��Ʒ����������y��Ԫ�������۵�����x��Ԫ֮��ĺ�����ϵ��
�������۵���Ϊ����Ԫʱ��B��Ʒÿ����������������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������ߵĶԳ�����x=1����x�����������㣬��y��Ľ��������ǣ�0��3������������ƽ��2����λ���Ⱥõ��µ������ߵĽ���ʽ��y=ax2+bx+c�������ĸ����ۣ�
��b2��4ac��0����abc��0����4a+2b+c=1����a��b+c��0�У�������ȷ����_____������ţ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
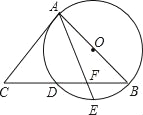
����Ŀ����ͼ��AB�ǡ�O��ֱ����BC����O�ڵ�D��E��![]() ���е㣬AE��BC���ڵ�F����C=2��EAB��
���е㣬AE��BC���ڵ�F����C=2��EAB��
��1����֤��AC�ǡ�O�����ߣ�
��2����֪CD=4��CA=6��
����CB�ij���
����DF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�������żܿ��Խ��ƿ������ɵ�������ABD8D1�����Ϸ���������D1OD8���.��������ͼ��ʾ��ֱ������ϵ�����AB=44�ף���A=45�㣬AC1=4�ף���D2������Ϊ(-13��-1.69)�����żܵĹ���OH=________��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��Ԥ��������H1N1����ijУ�Խ��Ҳ���ҩ������������������֪ҩ��ȼ��ʱ������ÿ���������еĺ�ҩ��y��mg����ʱ��x��min������������ҩ��ȼ�պ�y��x�ɷ���������ͼ��ʾ���ֲ��ҩ��8minȼ�ϣ���ʱ���ڿ���ÿ�����ĺ�ҩ��Ϊ6mg��������������ṩ����Ϣ������������⣺
��1��ҩ��ȼ��ʱ����y����x�ĺ�����ϵʽ���Ա���x��ȡֵ��Χ��ʲô��ҩ��ȼ�պ�y��x�ĺ�����ϵʽ�أ�
��2���о���������������ÿ�����ĺ�ҩ������1.6mgʱ�������ɽ����ң���ô��������ʼ��������Ҫ�����Ӻ������ܽ�����ң�
��3���о���������������ÿ�����ĺ�ҩ��������3mg�ҳ���ʱ�䲻����10minʱ������ɱ������еĶ�����ô��������Ƿ���Ч��Ϊʲô��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���Ե�OΪԲ�ĵ�����ͬ��Բ�У���Բ����AB��СԲ�ڵ�C��D����ͼ����
��1����֤��AC=BD��
��2������Բ�İ뾶R=10��СԲ�İ뾶r=8����ԲO��ֱ��AB�ľ���Ϊ6����AC�ij���

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com