
 如图,在△ABC中,D是AC的中点,E,F在BC上,且BE=EF=FC,AE与BD交于点M,G是AE的中点,DF与CG交于点N,求证:MN∥BC.
如图,在△ABC中,D是AC的中点,E,F在BC上,且BE=EF=FC,AE与BD交于点M,G是AE的中点,DF与CG交于点N,求证:MN∥BC. 分析 连接DG,根据三角形的中位线定理得到BM=DM,通过三角形全等得到GM=ME,再根据三角形的中位线定理即可得到结果.
解答 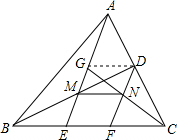 证明:连接DG,
证明:连接DG,
∵AG=GE,AD=DC,
∴DG∥EC,
∴∠MBE=∠MDG,
∵EF=FC,AD=DC,
∴DF∥AE,
∵ME∥DF,BE=EF,
∴BM=DM,
在△BME与DMG中,$\left\{\begin{array}{l}{∠MBE=∠MDG}\\{BM=DM}\\{∠BME=∠GMD}\end{array}\right.$,
∴△BME≌△DMG,
∴GM=ME,
∵DF∥AE,AD=DC,
∴GN=NC,GM=ME,
∴MN∥EC,
∴MN∥BC.
点评 本题考查了三角形的中位线定理,平行线的性质,全等三角形的判定与性质,掌握三角形的中位线定理是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,已知线段a和b,a>b,求作直角三角形ABC,使直角三角形的斜边AB=a,直角边AC=b.(用尺规作图,保留作图痕迹,不要求写作法)
如图,已知线段a和b,a>b,求作直角三角形ABC,使直角三角形的斜边AB=a,直角边AC=b.(用尺规作图,保留作图痕迹,不要求写作法)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
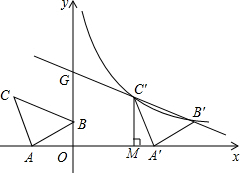 如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-2,0)、B(0,d)、C(-3,2).
如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-2,0)、B(0,d)、C(-3,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
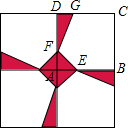 一个边长为8m的正方形花坛由4块全等的小正方形组成,在小正方形ABCD中,点G、E、F分别在CD、AB、AD上,且DG=1m,AE=AF,在△AEF、△DFG、五边形EBCGF三个区域上种植不同的花卉,每平方米的种植成本分别是20元、20元、10元,问点E在什么位置时,正方形花坛种植花卉所需的总费用是715元?
一个边长为8m的正方形花坛由4块全等的小正方形组成,在小正方形ABCD中,点G、E、F分别在CD、AB、AD上,且DG=1m,AE=AF,在△AEF、△DFG、五边形EBCGF三个区域上种植不同的花卉,每平方米的种植成本分别是20元、20元、10元,问点E在什么位置时,正方形花坛种植花卉所需的总费用是715元?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 每公顷所需生产组/个 | 每公顷雨季产值 | |
| 蔬菜 | $\frac{1}{2}$ | 52500 |
| 水稻 | $\frac{1}{4}$ | 18000 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
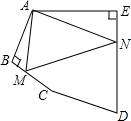 如图,在五边形ABCDE中,∠BAE=120°,∠B=∠E=90°,AB=BC,AE=DE,在BC,DE上分别找出一点M,N,使得△AMN的周长最小时,则∠AMN+∠ANM的度数为多少?
如图,在五边形ABCDE中,∠BAE=120°,∠B=∠E=90°,AB=BC,AE=DE,在BC,DE上分别找出一点M,N,使得△AMN的周长最小时,则∠AMN+∠ANM的度数为多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com