
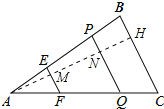
【题目】如图,△ABC中,点E、P在边AB上,且AE=BP,过点E、P作BC的平行线,分别交AC于点F、Q,记△AEF的面积为S1,四边形EFQP的面积为S2,四边形PQCB的面积为S3.

(1)求证:EF+PQ=BC;
(2)若S1+S3=S2,求![]() 的值;
的值;
(3)若S3﹣S1=S2,直接写出![]() 的值.
的值.
【答案】(1)见解析;(2)2;(3)![]() .
.
【解析】
试题分析:(1)由平行线得出比例式![]() ,
,![]() ,证出AP=BE,得出
,证出AP=BE,得出![]() =1,即可得出EF+PQ=BC;
=1,即可得出EF+PQ=BC;
(2)过点A作AH⊥BC于H,分别交PQ于M、N,设EF=a,PQ=b,AM=h,则BC=a+b,由平行线得出△AEF∽△APQ,得出![]() =
=![]() ,得出AN=
,得出AN=![]() ,MN=(
,MN=(![]() ﹣1)h,
﹣1)h,
由三角形的面积公式得出S1=![]() ah,S2=
ah,S2=![]() (a+b)(
(a+b)(![]() ﹣1)h,S3=
﹣1)h,S3=![]() (b+a+b)h,得出
(b+a+b)h,得出![]() ah+
ah+![]() (a+b+b)h=
(a+b+b)h=![]() (a+b)(
(a+b)(![]() ﹣1)h,求出b=3a,即可得出结果;(3)由题意得出
﹣1)h,求出b=3a,即可得出结果;(3)由题意得出![]() (a+b+b)h﹣
(a+b+b)h﹣![]() ah=
ah=![]() (a+b)(
(a+b)(![]() ﹣1)h,得出b=(1+
﹣1)h,得出b=(1+![]() )a,即可得出结果.
)a,即可得出结果.
(1)证明:∵EF∥BC,PQ∥BC,
∴![]() ,
,![]() ,
,
∵AE=BP,
∴AP=BE,
∴![]() =
=![]() =1,
=1,
∴![]() =1,
=1,
∴EF+PQ=BC;
(2)解:过点A作AH⊥BC于H,分别交PQ于M、N,如图所示:
设EF=a,PQ=b,AM=h,
则BC=a+b,
∵EF∥PQ,
∴△AEF∽△APQ,
∴![]() =
=![]() ,
,
∴AN=![]() ,MN=(
,MN=(![]() ﹣1)h,
﹣1)h,
∴S1=![]() ah,S2=
ah,S2=![]() (a+b)(
(a+b)(![]() ﹣1)h,S3=
﹣1)h,S3=![]() (b+a+b)h,
(b+a+b)h,
∵S1+S3=S2,
∴![]() ah+
ah+![]() (a+b+b)h=
(a+b+b)h=![]() (a+b)(
(a+b)(![]() ﹣1)h,
﹣1)h,
解得:b=3a,
∴![]() =3,
=3,
∴![]() =2;
=2;
(3)解:∵S3﹣S1=S2,
∴![]() (a+b+b)h﹣
(a+b+b)h﹣![]() ah=
ah=![]() (a+b)(
(a+b)(![]() ﹣1)h,
﹣1)h,
解得:b=(1±![]() )a(负值舍去),
)a(负值舍去),
∴b=(1+![]() )a,
)a,
∴![]() =1+
=1+![]() ,
,
∴![]() =
=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】为了响应国家节能减排的号召,鼓励市民节约用电,我市从2012年7月1日起,居民用电实行“一户一表”的“阶梯电价”,分三个档次收费,第一档是用电量不超过180千瓦时实行“基本电价”,第二、三档实行“提高电价”,具体收费情况如下折线图,请根据图象回答下列问题;

(1)当用电量是180千瓦时时,电费是 元;
(2)第二档的用电量范围是 ;
(3)“基本电价”是 元/千瓦时;
(4)小明家8月份的电费是328.5元,这个月他家用电多少千瓦时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面解答过程,填空或填理由.
已知如图,点E,F分别是AB和CD上的点,DE,AF分别交BC于点G,H,∠A=∠D,∠1=∠2.试说明:∠B=∠C.

解:∵∠1=∠2 ( ),
∠2=∠3 ( ),
∴∠3=∠1 ( ).
∴AF∥DE ( ).
∴∠4=∠D ( ).
又∵∠A=∠D ( ),
∴∠A=∠4 ( ).
∴AB∥CD ( ).
∴∠B=∠C ( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A. 有一个角为直角的四边形是菱形
B. 对角线互相垂直的菱形是正方形
C. 对角线相等的平行四边形是矩形
D. 一组邻边相等的平行四边形是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=a(x+4)(x﹣6)与x轴交于A,B两点(点A在B的左侧),顶点为P,且点P在直线y=2x+m上.
(1)试用含m的代数式表示a;
(2)若△ABP为直角三角形,试求该抛物线和直线的函数表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com