
【题目】如图所示,平面直角坐标系xOy中,矩形ABCD的边AB=4,BC=6.在不改变矩形ABCD的形状和大小的情况下,当矩形的顶点A在x轴的正半轴上左右移动时,另一个顶点D始终在y轴的正半轴上随之上下移动.
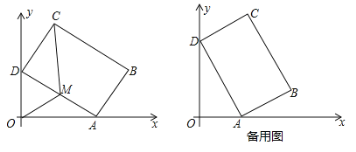
(1)当∠OAD=30°时,求点C的坐标;
(2)设AD的中点为M,连接OM、MC,若四边形OMCD的面积为![]() 时,求OA的长;
时,求OA的长;
(3)在点A移动过程中是否存在某一位置,使点C到点O的距离有最大值?若存在,求此时的值;若不存在,请说明理由.
【答案】(1)点![]() 的坐标为
的坐标为![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]() 的最大值为8.
的最大值为8.
【解析】
(1)作CE⊥y轴,先证∠CDE=∠OAD=30°得CE=![]() CD=2,DE=
CD=2,DE=![]() ,再由∠OAD=30°知OD=
,再由∠OAD=30°知OD=![]() AD=3,从而得出点C坐标;
AD=3,从而得出点C坐标;
(2)先求出S△DCM=6,结合S四边形OMCD=![]() 知S△ODM=
知S△ODM=![]() ,S△OAD=9,设OA=x、OD=y,据此知x2+y2=36,
,S△OAD=9,设OA=x、OD=y,据此知x2+y2=36,![]() xy=9,得出x2+y2=2xy,即x=y,代入x2+y2=36求得x的值,从而得出答案;
xy=9,得出x2+y2=2xy,即x=y,代入x2+y2=36求得x的值,从而得出答案;
(3)由M为AD的中点,知OM=3,CM=5, OM+CM=8,分两种情况,即当O、M、C三点不在同一条直线和三点共线时,分别进行判断解决即可.
(1)如图1,过点C作CE⊥y轴于点E,
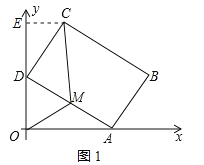
∵矩形ABCD中,CD⊥AD,
∴∠CDE+∠ADO=90°,
又∵∠OAD+∠ADO=90°,
∴∠CDE=∠OAD=30°,
∴在Rt△CED中,CE=![]() CD=2,DE=
CD=2,DE=![]() =2
=2![]() ,
,
在Rt△OAD中,∠OAD=30°,
∴OD=![]() AD=3,
AD=3,
∴点C的坐标为(2,3+2![]() );
);
(2)∵M为AD的中点,
∴DM=3,S△DCM=6,
又S边形OMCD=![]() ,
,
∴S△ODM=![]() ,
,
∴S△OAD=9,
设OA=x、OD=y,则x2+y2=36,![]() xy=9,
xy=9,
∴x2+y2=2xy,即x=y,
将x=y代入x2+y2=36得x2=18,
解得x=3![]() (负值舍去),
(负值舍去),
∴OA=3![]() ;
;
(3)OC的最大值为8,
如图2,M为AD的中点,

∴OM=3,CM=![]() =5,
=5,
∴OM+CM=8.
当O、M、C三点不在同一条直线时,在△OCM中,
OC<OM+CM=8.
当A点运动,使得O、M、C三点在同一直线时,
此时OC= OM+CM=8,为OC的最大值.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
【题目】2020年,新型冠状病毒席卷全球,疫情当前,全国上下砥砺同行.某中学校指导中心为引导未成年人以健康心理、阳光心态抗击疫情,积极开展了心理援助工作,并推出“你是我的奥特曼”有奖征稿活动.活动结束后,该指导中心对参赛学生的获奖情况进行统计,并绘制了如下两幅不完整的统计图.
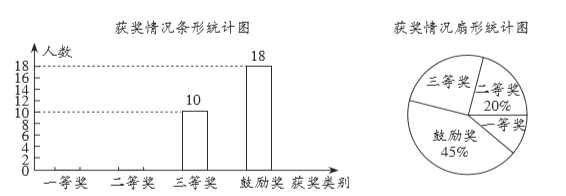
结合图中的相关数据,解答下列问题:
(1)参加此次有奖征稿活动的学生有 人,在扇形统计图中,“三等奖”所对应扇形的圆心角度数为 ;
(2)将条形统计图补充完整;
(3)若获得“一等奖”的学生中有![]() 来自七年级,
来自七年级,![]() 来自九年级,其余来自八年级,学校决定从获得“一等奖”的学生中任选2名作为代表在线上分享心灵战“疫”小锦囊,请用列表或画树状图的方法求所选2名学生中恰好是1名七年级和1名九年级学生的概率.
来自九年级,其余来自八年级,学校决定从获得“一等奖”的学生中任选2名作为代表在线上分享心灵战“疫”小锦囊,请用列表或画树状图的方法求所选2名学生中恰好是1名七年级和1名九年级学生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
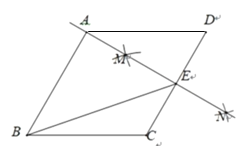
【题目】如图,在菱形ABCD中,按以下步骤作图:
①分别以点C和点D为圆心,大于![]() 的同样的长为半径作弧,两弧交于M,N两点;
的同样的长为半径作弧,两弧交于M,N两点;
②作直线MN,交CD于点E,连接BE.
若直线MN恰好经过点A,则下列说法错误的是( )
A.ABC60°
B.![]()
C.若AB4,则BE![]()
D.tanCBE![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售![]() 型和
型和![]() 型两种学习机,其中用10000元采购
型两种学习机,其中用10000元采购![]() 型学习机台数和用8000元采购
型学习机台数和用8000元采购![]() 型学习机台数相等,且一台
型学习机台数相等,且一台![]() 型学习机比一台
型学习机比一台![]() 型学习机进价多100元.
型学习机进价多100元.
(1)求一台![]() 型和
型和![]() 型学习机价格各是多少元?
型学习机价格各是多少元?
(2)若购进![]() 型学习机共100台,其中
型学习机共100台,其中![]() 型的进货量不超过
型的进货量不超过![]() 型的2倍,设购进
型的2倍,设购进![]() 型学习机
型学习机![]() 台.
台.
①求![]() 的取值范围.
的取值范围.
②已知![]() 型学习机售价均是900元/台,实际进货时,厂家对
型学习机售价均是900元/台,实际进货时,厂家对![]() 型学习机在原进货价的基础,上下调
型学习机在原进货价的基础,上下调![]() 元,且限定商店最多购进
元,且限定商店最多购进![]() 型学习机60台,若商店保持同种学习机的售价不变,请你根据以上信息,求出使这100台学习机销售总利润
型学习机60台,若商店保持同种学习机的售价不变,请你根据以上信息,求出使这100台学习机销售总利润![]() (元)的最大值.
(元)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为向明中学提供午餐的某送餐公司计划每月最后一天推出学生“惊喜套餐”,现做出几款套餐后打算每班邀请一位学生代表来品尝.初三(6)班有44人(学号从1~44号),班长设计了一个推选本班代表的办法:从一副扑克牌中选取了分别标有数字1、2、3、4的四张牌.先抽取一张牌记下数字后,放回洗匀;再抽取一张牌记下数字,两个数字依次组成学生代表的学号.比如第一张抽到1,第二张抽到4,就是学号为14的这个同学作为本班代表.
(1)如果小林的学号为23,请用列表法或画出树状图的方法,求出他被抽到的概率;
(2)对初三(6)班的每位同学来说,班长设计的办法是否公平?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在四边形ABCD中,AB⊥AC,DC⊥AC,∠B=∠D,![]() ,
,![]() ,
,![]() ,点E,F分别是BC,AD的中点.
,点E,F分别是BC,AD的中点.
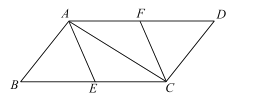
(1)求证:![]() ;
;
(2)当![]() 与
与![]() 满足什么数量关系时,四边形
满足什么数量关系时,四边形![]() 是正方形?请证明.
是正方形?请证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市一段时期内对某种商品经销情况进行统计得到该商品的销售数量![]() (件)由基础销售量与浮动销售量两个部分组成,其中基本销售量保持不变,浮动销售量与售价
(件)由基础销售量与浮动销售量两个部分组成,其中基本销售量保持不变,浮动销售量与售价![]() (元/件,
(元/件,![]() )成反比例,销售过程中得到的部分数据如下:
)成反比例,销售过程中得到的部分数据如下:
售价 | 8 | 10 |
销售数量 | 70 | 58 |
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)当该商品销售数量为50件时,求每件商品的售价;
(3)设销售总额为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
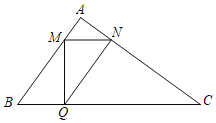
【题目】如图,在ABC中,∠A=90°,AB=3,AC=4,点M、Q分别是边AB、BC上的动点(点M不与A、B重合),且MQ⊥BC,过点M作MN∥BC.交AC于点N,连接NQ,设BQ=x.
(1)是否存在一点Q,使得四边形BMNQ为平行四边形,并说明理由;
(2)当BM=2时,求x的值;
(3)当x为何值时,四边形BMNQ的面积最大,并求出最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
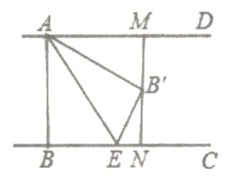
【题目】如图,已知![]() ,点
,点![]() 为射线
为射线![]() 上一个动点,连接
上一个动点,连接![]() ,将
,将![]() 沿
沿![]() 折叠,点
折叠,点![]() 落在点
落在点![]() 处,过点
处,过点![]() 作
作![]() 的垂线,分别交
的垂线,分别交![]() 于点
于点![]() 当点
当点![]() 为线段
为线段![]() 的三等分点时,
的三等分点时,![]() 的长为_____________
的长为_____________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com