
【题目】如图,在△ABC中,AD⊥BC于D,AE平分∠BAC.
(1)若∠B=30°,∠C=70°,则∠DAE=
(2)若∠C﹣∠B=30°,则∠DAE= .
(3)若∠C﹣∠B=α(∠C>∠B),求∠DAE的度数(用含α的代数式表示).

【答案】(1)20°;(2)15°;(3)∠DAE=![]() α.
α.
【解析】
(1)根据垂直定义由AD⊥BC得∠ADC=90°,再利用角平分线定义得∠EAC=![]() ∠BAC,然后根据三角形内角和定理得∠BAC=180°﹣∠B﹣∠C,∠DAC=90°﹣∠C,则∠DAE=
∠BAC,然后根据三角形内角和定理得∠BAC=180°﹣∠B﹣∠C,∠DAC=90°﹣∠C,则∠DAE=![]() (∠C﹣∠B),代入计算即可.
(∠C﹣∠B),代入计算即可.
(2)利用(1)中结论代入计算即可.
(3)利用(1)中结论代入计算即可.
解:(1)∵AD⊥BC于D,
∴∠ADC=90°,
∵AE平分∠BAC,
∴∠EAC=![]() ∠BAC,
∠BAC,
而∠BAC=180°﹣∠B﹣∠C,
∴∠EAC=90°﹣![]() ∠B﹣
∠B﹣![]() ∠C,
∠C,
∵∠DAC=90°﹣∠C,
∴∠DAE=∠EAC﹣DAC
=90°﹣![]() ∠B﹣
∠B﹣![]() ∠C﹣(90°﹣∠C)
∠C﹣(90°﹣∠C)
=![]() (∠C﹣∠B),
(∠C﹣∠B),
若∠B=30°,∠C=70°,则∠DAE=![]() (70°﹣30°)=20°;
(70°﹣30°)=20°;
(2)若∠C﹣∠B=30°,则∠DAE=![]() ×34°=15°.
×34°=15°.
(3)若∠C﹣∠B=α(∠C>∠B),则∠DAE=![]() α.
α.
故答案为20°,15°.


科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=6cm,BC=4cm,点D为AB的中点.
⑴如果点P在线段BC上以1cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CPQ是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为______cm/s时,在某一时刻也能够使△BPD与△CPQ全等.
⑵若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都按逆时针方向沿△ABC的三边运动.求经过多少秒后,点P与点Q第一次相遇,并写出第一次相遇点在△ABC的哪条边上?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正比例函数和反比例函数的图象都经过点 A(3,3).
(1)求正比例函数和反比例函数的解析式;
(2)把直线 OA 向下平移后得到直线 l,与反比例函数的图象交于点 B(6,m),求 m 的值和直线 l 的解 析式;
(3)在(2)中的直线 l 与 x 轴、y 轴分别交于 C、D,求四边形 OABC 的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
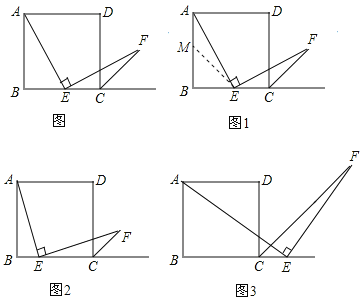
【题目】如图,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角平分线CF于点F.请你认真阅读下面关于这个图的探究片段,完成所提出的问题.
(1)探究1:小强看到图(*)后,很快发现AE=EF,这需要证明AE和EF所在的两个三角形全等,但△ABE和△ECF显然不全等(一个是直角三角形,一个是钝角三角形),考虑到点E是边BC的中点,因此可以选取AB的中点M,连接EM后尝试着去证△AEM≌EFC就行了,随即小强写出了如下的证明过程:
证明:如图1,取AB的中点M,连接EM.
∵∠AEF=90°
∴∠FEC+∠AEB=90°
又∵∠EAM+∠AEB=90°
∴∠EAM=∠FEC
∵点E,M分别为正方形的边BC和AB的中点
∴AM=EC
又可知△BME是等腰直角三角形
∴∠AME=135°
又∵CF是正方形外角的平分线
∴∠ECF=135°
∴△AEM≌△EFC(ASA)
∴AE=EF
(2)探究2:小强继续探索,如图2,若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点”,其余条件不变,发现AE=EF仍然成立,请你证明这一结论.
(3)探究3:小强进一步还想试试,如图3,若把条件“点E是边BC的中点”改为“点E是边BC延长线上的一点”,其余条件仍不变,那么结论AE=EF是否成立呢?若成立请你完成证明过程给小强看,若不成立请你说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4个完全相同的小球,分别标有数字1、2、3、4,另有一个可以自由旋转的圆盘.被分成面积相等的3个扇形区,分别标有数字1、2、3(如图所示).小颖和小亮想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一个人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于4,那么小颖去;否则小亮去.
(1)用树状图或列表法求出小颖参加比赛的概率;
(2)你认为该游戏公平吗?请说明理由;若不公平,请修改该游戏规则,使游戏公平.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点E在⊙O上,C为![]() 的中点,过点C作直线CD⊥AE于D,连接AC,BC.
的中点,过点C作直线CD⊥AE于D,连接AC,BC.

(1)试判断直线CD与⊙O的位置关系,并说明理由;
(2)若AD=2,AC=![]() ,求AB的长.
,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是小华同学一个学期数学成绩的记录.根据表格提供的信息,回答下列的问题:
考试类别 | 平时考试 | 期中考试 | 期末考试 | |||
第一单元 | 第二单元 | 第三单元 | 第四单元 | |||
成绩(分) | 85 | 78 | 90 | 91 | 90 | 94 |
(1)小明6次成绩的众数是 ,中位数是 ;
(2)求该同学这个同学这一学期平时成绩的平均数;
(3)总评成绩权重规定如下:平时成绩占20%,期中成绩占30%,期末成绩占50%,请计算出小华同学这一个学期的总评成绩是多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市一水果销售公司,需将一批鲜桃运往某地,有汽车、火车、运输工具可供选择,两种运输工具的主要参考数据如下:
运输工具 | 途中平均速度(单位:千米/时) | 途中平均费用(单位:元/千米) | 装卸时间(单位:小时) | 装卸费用(单位:元) |
汽车 | 75 | 8 | 2 | 1000 |
火车 | 100 | 6 | 4 | 2000 |
若这批水果在运输过程中(含装卸时间)的损耗为150元/时,设运输路程为x(![]() )千米,用汽车运输所需总费用为y1元,用火车运输所需总费用为y2元.
)千米,用汽车运输所需总费用为y1元,用火车运输所需总费用为y2元.
(1)分别求出y1、y2与x的关系式;
(2)那么你认为采用哪种运输工具比较好?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点E在⊙O上,C为![]() 的中点,过点C作直线CD⊥AE于D,连接AC,BC.
的中点,过点C作直线CD⊥AE于D,连接AC,BC.

(1)试判断直线CD与⊙O的位置关系,并说明理由;
(2)若AD=2,AC=![]() ,求AB的长.
,求AB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com