
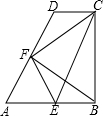
 如图,在直角梯形ABCD中,AB∥DC,AB⊥BC,∠A=60°,AB=2CD,E、F分别为AB、AD的中点,连接EF、EC、BF、CF.则①四边形AECD为平行四边形;②△AEF为等边三角形;③△FDC与△BEF为全等的等腰三角形;④△AFB≌△EFC,其中正确的结论有①②③④(写出正确的序号即可)
如图,在直角梯形ABCD中,AB∥DC,AB⊥BC,∠A=60°,AB=2CD,E、F分别为AB、AD的中点,连接EF、EC、BF、CF.则①四边形AECD为平行四边形;②△AEF为等边三角形;③△FDC与△BEF为全等的等腰三角形;④△AFB≌△EFC,其中正确的结论有①②③④(写出正确的序号即可) 分析 ①由AB=2CD,E为AB的中点,可得AE=CD,又AB∥DC,根据有一组对边平行且相等的四边形是平行四边形可得四边形AECD为平行四边形,从而判断①正确;
②连结DE.由BE=CD,BE∥CD,∠EBC=90°,可得四边形EBCD是矩形,那么可求∠AED=90°,又F为AD的中点,根据直角三角形斜边的中线等于斜边的一半得到EF=AF=DF=$\frac{1}{2}$AD,又∠A=60°,根据有一个角是60°的等腰三角形是等边三角形可得△AEF为等边三角形,从而判断②正确;
③先证明DF=CD=BE=EF,得出△FDC与△BEF都为等腰三角形.再根据SAS证明△FDC≌△BEF,那么△FDC与△BEF为全等的等腰三角形,从而判断③正确;
④根据SAS即可证明△AFB≌△EFC,从而判断④正确.
解答 解:①∵AB=2CD,E为AB的中点,即AB=2AE=2BE,
∴AE=CD,
∵AB∥DC,
∴四边形AECD为平行四边形,故①正确;
②连结DE.
∵BE=CD,BE∥CD,∠EBC=90°,
∴四边形EBCD是矩形,
∴∠BED=90°,
∴∠AED=90°,
∵F为AD的中点,
∴EF=AF=DF=$\frac{1}{2}$AD,
∵∠A=60°,
∴△AEF为等边三角形,故②正确;
③∵△AEF为等边三角形,
∴AE=EF=AF,∠AEF=60°,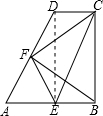 ∵AF=DF,AE=BE=CD,
∵AF=DF,AE=BE=CD,
∴DF=CD=BE=EF,
∴△FDC与△BEF都为等腰三角形.
在△FDC与△BEF中,
$\left\{\begin{array}{l}{DF=EB}\\{∠FDC=∠BEF=120°}\\{DC=EF}\end{array}\right.$,
∴△FDC≌△BEF(SAS),
∴△FDC与△BEF为全等的等腰三角形,故③正确;
④∵四边形AECD为平行四边形,
∴CE∥AD,
∴∠CEB=∠A=60°,
∴∠FEC=180°-∠AEF-∠CEB=180°-60°-60°=60°,
∵∠EBC=90°,
∴∠ECB=30°,
∴BE=$\frac{1}{2}$EC,EC=2BE,
∵AB=2BE,
∴AB=EC.
在△AFB与△EFC中,
$\left\{\begin{array}{l}{AF=EF}\\{∠A=∠FEC=60°}\\{AB=EC}\end{array}\right.$,
∴△AFB≌△EFC(SAS),故④正确.
故答案为①②③④.
点评 本题是四边形综合题,其中涉及到平行四边形、矩形、全等三角形的判定与性质,等边三角形、等腰三角形的判定,直角三角形的性质等知识,综合性较强,难度适中.准确作出辅助线利用数形结合是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
| A型车 | B型车 | |
| 进货价格(元) | 1100 | 1400 |
| 销售价格(元) | 今年的销售价格 | 2000 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知第一象限内的点A在反比例函数y=$\frac{2}{x}$的图象上,第二象限内的点B在反比例函数y=$\frac{k}{x}$的图象上,且OA⊥OB,tanA=$\sqrt{3}$,则k的值为-6.
如图,已知第一象限内的点A在反比例函数y=$\frac{2}{x}$的图象上,第二象限内的点B在反比例函数y=$\frac{k}{x}$的图象上,且OA⊥OB,tanA=$\sqrt{3}$,则k的值为-6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
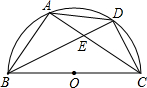 如图,BC是半圆O的直径,D是弧AC的中点,四边形ABCD的对角线AC、BD交于点E,CE=$\sqrt{5}$,CD=2.
如图,BC是半圆O的直径,D是弧AC的中点,四边形ABCD的对角线AC、BD交于点E,CE=$\sqrt{5}$,CD=2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com