
 ��ͼ����ƽ��ֱ������ϵ�У���A��1��1��Ϊ�����������y=x2-2x+c��y�ύ�ڵ�C��������ABCD�ı�CD��y���غϣ���PΪ��һ�������������ϵĵ��Ҳ����A�غϣ�����P��PF��x�ύy���ڵ�F��PE��y�ύx���ڵ�E�����P�ĺ�����Ϊm������PFOE��������ABCD�ص�����ͼ�ε��ܳ�ΪL��
��ͼ����ƽ��ֱ������ϵ�У���A��1��1��Ϊ�����������y=x2-2x+c��y�ύ�ڵ�C��������ABCD�ı�CD��y���غϣ���PΪ��һ�������������ϵĵ��Ҳ����A�غϣ�����P��PF��x�ύy���ڵ�F��PE��y�ύx���ڵ�E�����P�ĺ�����Ϊm������PFOE��������ABCD�ص�����ͼ�ε��ܳ�ΪL������ ��1������A��1��1�����������߽���ʽ�������cֵ��
��2��������PFOE������������ߵĶԳ���ƽ��ʱ����P��F���������ߵĶԳ���Գƣ��������ߵĶ������꼴�ɵó������ߵĶԳ���Ϊx=1����ϵ�F�ĺ�����Ϊ0�����ɵó�m��ֵ��
��3���ɵ�P�ĺ�����Ϊm���ҳ���P��F�����꣬�ɴ˼��ɵó�PF��FD�ij��ȣ���0��m��1��1��m��1������������ݾ��ε��ܳ���ʽ���ɵó�L����m�ĺ�����ϵʽ��
��4������BD���ɵ�B��D�����꼴�ɵó�ֱ��BD�ĺ�������ʽ������ֱ��BD�������߽���ʽ�ɷ����飬����������꣬�ɴ˿ɷ�0��m��$\frac{3-\sqrt{5}}{2}$��$\frac{3-\sqrt{5}}{2}$��m��1��1��m��2�Լ�m��2����������ǣ���������ε������Լ�����ֱ�������ε��ж����ɵó����ۣ�
��� �⣺��1������A��1��1������y=x2-2x+c�У�
�ã�1=1-2+c����ã�c=2��
�ʴ�Ϊ��2��
��2����PE��y�ᣬ����PFOE������������ߵĶԳ���ƽ�֣�
��P��F����������ߵĶԳ���Գƣ�
�������ߵĶ�������Ϊ��1��1����
�������ߵĶԳ���Ϊx=1��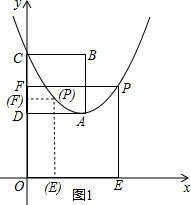
��F��ĺ�����Ϊ0��
��m=2��
��3���ߵ�P�ĺ�����Ϊm����PΪ��һ�������������ϵĵ��Ҳ����A�غϣ�
��P��m��m2-2m+2����m��0����m��1����
���ı���ABCDΪ�����Σ���A��1��1����
��D��0��1����B��1��2����F��0��m2-2m+2����
��PF=m��FD=m2-2m+2-1=m2-2m+1��
���ݵ�P�ڵ�A�����Ҳ�ͬ�������������ͼ1����
��0��m��1ʱ��L=2����PF+FD��=2����m+m2-2m+1��=2m2-2m+2��
��1��m��2ʱ��L=2����AD+FD��=2����1+m2-2m+1��=2m2-4m+4��
��4������BD����ͼ2��ʾ��
��ֱ��BD�Ľ���ʽΪy=kx+b��
��D��0��1����B��1��2������y=kx+b��
�ã�$\left\{\begin{array}{l}{b=1}\\{k+b=2}\end{array}\right.$����ã�$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$��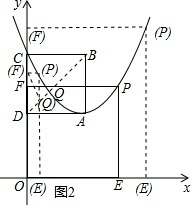
��ֱ��BD�Ľ���ʽΪy=x+1��
����ֱ��AB�������߽���ʽ�ã�$\left\{\begin{array}{l}{y=x+1}\\{y={x}^{2}-2x+2}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{x=\frac{3-\sqrt{5}}{2}}\\{y=\frac{5-\sqrt{5}}{2}}\end{array}\right.$��$\left\{\begin{array}{l}{x=\frac{3+\sqrt{5}}{2}}\\{y=\frac{5+\sqrt{5}}{2}}\end{array}\right.$����ȥ����
��0��m��$\frac{3-\sqrt{5}}{2}$ʱ����Ҫ��FDQΪ����ֱ�������Σ�
ֻ��FD=$\sqrt{2}$DQ=2PF����m2-2m+1=4m��
��ã�m=$\frac{5-\sqrt{21}}{2}$��m=$\frac{5+\sqrt{21}}{2}$����ȥ����
��$\frac{5-\sqrt{21}}{2}$��$\frac{3-\sqrt{5}}{2}$��
���ʱ����FDQ��Ϊ����ֱ�������Σ�
��$\frac{3-\sqrt{5}}{2}$��m��1ʱ��
���ı���ABCDΪ�����Σ�
���FDQ=��CDB=45�㣬
�ߡ�DFQ=90�㣬
���FDQΪ����ֱ�������Σ�
��1��m��2ʱ��
���ı���ABCDΪ�����Σ�
���FDQ=��CDB=45�㣬
�ߡ�DFQ=90�㣬
���FDQΪ����ֱ�������Σ�
��m��2ʱ���߶�BD�����PFOE�ı�ֻ��һ������D��û�е�Q��
����ڡ�FDQ��
���Ͽ�֪������FDQΪ����ֱ��������ʱ��m��ȡֵ��ΧΪ$\frac{3-\sqrt{5}}{2}$��m��1��1��m��2��
���� ���⿼���˴���ϵ������������ʽ�����ε����ʡ����ε��ܳ��������ε������Լ�����ֱ�������ε��ж�������Ĺؼ��ǣ���1�����ô���ϵ�������c����2�����ݶԳ������m����3����0��m��1��1��m��1������������þ��ε��ܳ���ʽ���L����m�ĺ�����ϵʽ����4����0��m��$\frac{3-\sqrt{5}}{2}$��$\frac{3-\sqrt{5}}{2}$��m��1��1��m��2�Լ�m��2����������ǣ����������е��⣬�ڣ�4��С���ѶȲ�С���ڽ�������У�Ӧ��ֿ���m���ٽ�㣬��$\frac{3-\sqrt{5}}{2}$��1��2������m��0�ֳ��Ķ������ǣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�O���ڽ��ı���ACDB�У�ABΪֱ����AC��BC=1��2����DΪ��AB���е㣬BE��CD����ΪE��
��ͼ���ڡ�O���ڽ��ı���ACDB�У�ABΪֱ����AC��BC=1��2����DΪ��AB���е㣬BE��CD����ΪE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-2��3�� | B�� | ��2��3�� | C�� | ��-2��-3�� | D�� | ��2��-3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
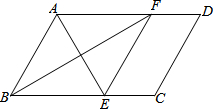 ��ͼ����?ABCD�У���BAD��ƽ���߽�BC�ڵ�E����ABC��ƽ���߽�AD�ڵ�F��
��ͼ����?ABCD�У���BAD��ƽ���߽�BC�ڵ�E����ABC��ƽ���߽�AD�ڵ�F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1.0��109 | B�� | 1.0��10-9 | C�� | -1.0��109 | D�� | -1.0��10-9 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com