
分析 根据三角形中位线的性质,可得到这个四边形是平行四边形,再由对角线垂直,能证出有一个角等于90°,则这个四边形为矩形.
解答 解:顺次连接一个四边形的各边中点,得到矩形的是;②菱形;④对角线互相垂直的四边形,
已知:AC⊥BD,E、F、G、H分别为各边的中点,连接点E、F、G、H.
求证:四边形EFGH是矩形,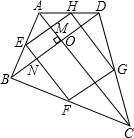
证明:∵E、F、G、H分别为各边的中点,
∴EF∥AC,GH∥AC,EH∥BD,FG∥BD,(三角形的中位线平行于第三边),
∴四边形EFGH是平行四边形,(两组对边分别平行的四边形是平行四边形),
∵AC⊥BD,EF∥AC,EH∥BD,
∴∠EMO=∠ENO=90°,
∴四边形EMON是矩形(有三个角是直角的四边形是矩形),
∴∠MEN=90°,
∴四边形EFGH是矩形(有一个角是直角的平行四边形是矩形).
故答案为:②④.
点评 本题考查的是矩形的判定方法,常用的方法有三种:①一个角是直角的平行四边形是矩形.②三个角是直角的四边形是矩形.③对角线相等的平行四边形是矩形.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源:2017届广东省梅州市九年级下学期第一次月考数学试卷(解析版) 题型:填空题
如图,△ABC中,AB=AC,DE垂直平分AB,BE⊥AC,AF⊥BC,则∠EFC=__°.
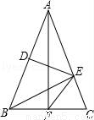
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6a3+2a2+1 | B. | 6a3-a2+1 | C. | 6a3+1 | D. | 6a3-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
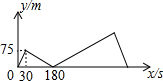 A、B两地相距1500米,甲从A地出发慢速跑向B地,30秒后乙从A地出发快速跑向B地,乙到B地后原地休息,在跑步的整个过程中,甲、乙两人的距离y(米)与甲出发的时间x(秒)之间的关系如图所示.
A、B两地相距1500米,甲从A地出发慢速跑向B地,30秒后乙从A地出发快速跑向B地,乙到B地后原地休息,在跑步的整个过程中,甲、乙两人的距离y(米)与甲出发的时间x(秒)之间的关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
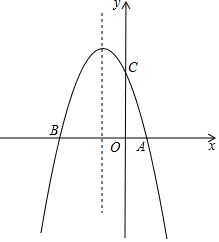 如图,抛物线y=-x2+bx+c与x轴交于A(1,0),B(-3,0)
如图,抛物线y=-x2+bx+c与x轴交于A(1,0),B(-3,0)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com