
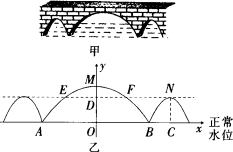
如图甲所示,三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小都相同.正常水位时,大孔水面宽度AB=20 m,顶点M距水面6 m(即MO=6 m),小孔顶点N距水面4.5 m(即NC=4.5 m).当水位上涨刚好淹没小孔时,借助图乙中的直角坐标系,求此时大孔的水面宽EF.
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com