
| A. | 1+(-2) | B. | 1-(-2) | C. | 1×(-2) | D. | 1÷(-2) |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在菱形ABCD中,tanA=$\sqrt{3}$,点E、F分别是AB、AD上任意的点(不与端点重合),且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H,给出如下几个结论:(1)△AED≌△DFB;(2)CG与BD一定不垂直;(3)∠BGE的大小为定值;(4)S四边形BCDG=$\frac{\sqrt{3}}{4}$CG2;其中正确结论的序号为(1)(3)(4).
如图,在菱形ABCD中,tanA=$\sqrt{3}$,点E、F分别是AB、AD上任意的点(不与端点重合),且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H,给出如下几个结论:(1)△AED≌△DFB;(2)CG与BD一定不垂直;(3)∠BGE的大小为定值;(4)S四边形BCDG=$\frac{\sqrt{3}}{4}$CG2;其中正确结论的序号为(1)(3)(4).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
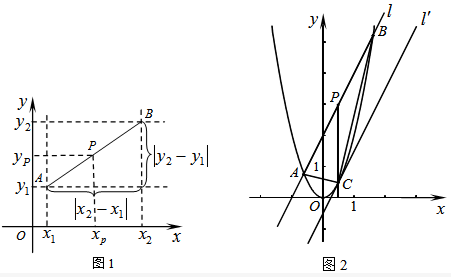
 已知,如图,抛物线y=ax2+x+c与x轴交于点A(-1,0),B(3,0).
已知,如图,抛物线y=ax2+x+c与x轴交于点A(-1,0),B(3,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
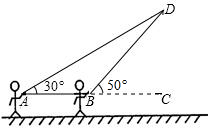 放风筝是大家喜爱的一种运动星期天的上午小明在金明广场上放风筝,如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝AD与水平线的夹角为30°,为了便于观察,小明迅速向前边移动,收线到达了离A处10米的B处,此时风筝线BD与水平线的夹角为50°,已知点A,B,C在同一条水平直线上,小明搬了一把梯子来取风筝,梯子能达到的最大高度为20米,请问小明能把风筝捡回来吗?(最后结果精确到1米)(风筝线AD,BD均为线段,$\sqrt{3}$≈1.732,sin50°≈0.766,cos50°≈0.643,tan50°≈1.192)
放风筝是大家喜爱的一种运动星期天的上午小明在金明广场上放风筝,如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝AD与水平线的夹角为30°,为了便于观察,小明迅速向前边移动,收线到达了离A处10米的B处,此时风筝线BD与水平线的夹角为50°,已知点A,B,C在同一条水平直线上,小明搬了一把梯子来取风筝,梯子能达到的最大高度为20米,请问小明能把风筝捡回来吗?(最后结果精确到1米)(风筝线AD,BD均为线段,$\sqrt{3}$≈1.732,sin50°≈0.766,cos50°≈0.643,tan50°≈1.192)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com