
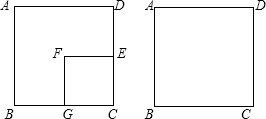
 道BG=DE,如果我们把正方形CGFE绕C点顺时钟旋转90度后,解决下列问题:
道BG=DE,如果我们把正方形CGFE绕C点顺时钟旋转90度后,解决下列问题: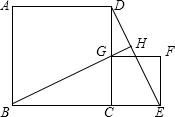
|


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
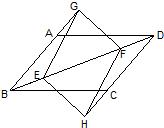 28、如图,E、F是平行四边形ABCD对角线BD上两点,BE=DF,点G、H分别在BA和DC的延长线上,且AG=CH,连接GE、EH、HF、FG.四边形GEHF是平行四边形吗?为什么?
28、如图,E、F是平行四边形ABCD对角线BD上两点,BE=DF,点G、H分别在BA和DC的延长线上,且AG=CH,连接GE、EH、HF、FG.四边形GEHF是平行四边形吗?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:
 12、如图所示,在四边形ABCD中,AD∥BC,BC>AD,∠B与∠C互余,将AB,CD分别平移到EF和EG的位置,则△EFG为
12、如图所示,在四边形ABCD中,AD∥BC,BC>AD,∠B与∠C互余,将AB,CD分别平移到EF和EG的位置,则△EFG为查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,四边形ABCD为正方形,曲线DEFGHIJ…叫做“正方形ABCD的渐开线”.其中
如图,四边形ABCD为正方形,曲线DEFGHIJ…叫做“正方形ABCD的渐开线”.其中 |
| DE |
 |
| EF |
 |
| FG |
 |
| GH |
 |
| HI |
 |
| IJ |
| π |
| 4 |
| 9 |
| 4 |
| 25 |
| 4 |
查看答案和解析>>
科目:初中数学 来源:101网校同步练习 初三数学 人教版(新课标2004年初审) 人教实验版 题型:022
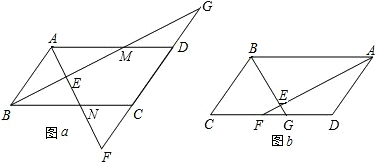
关于点M成中心对称的两个四边形ABCD和DEFG,AD、BE、CF、DG都经过点________,并被________点平分,则AB∥________,BC∥________,EF∥________,FG∥________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com