练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，将长方形OABC置于平面直角坐标系中，点A的坐标为(0，4)，点C的坐标为(m，0)(m>0)，点D(m，1)在BC上，将长方形OABC沿AD折叠压平，使点B落在坐标平面内，设点B的对应点为点E.

    （1）当m=3时，点B的坐标为_________，点E的坐标为_________; 

    （2）随着m的变化，试探索:点E能否恰好落在x轴上?若能，请求出m的值;若不能，请说明理由.

    （1）(3，4)，(0，1)；（2）点E能恰好落在x轴上，理由见解析. 【解析】试题分析：（1）根据点A、点D、点C的坐标和矩形的性质可以得到点B和点E的坐标； （2）由折叠的性质求得线段DE和AE的长，然后利用勾股定理得到有关m的方程，求得m的值即可． 试题解析：（1）点B的坐标为（3，4）， ∵AB=BD=3， ∴△ABD是等腰直角三角形， ∴∠BAD=45...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017-2018学年九年级数学北师大版上册 第3章 概率的进一步认识 单元测试卷 题型：解答题

    王老师将1个黑球和若干个白球(这些球除颜色外都相同)放入一个不透明的口袋并搅匀，让若干学生进行摸球实验，每次摸出1个球(有放回)，下表是活动进行中的一组统计数据.

    摸球的次数n

    100

    150

    200

    500

    800

    1000

    摸出黑球的次数m

    23

    31

    60

    130

    203

    251

    摸到黑球的频率

    0.23

    0.207

    0.30

    0.26

    0.254

    0.251

    (1)根据上表数据估计从袋中摸出1个球是黑球的概率是_________；

    (2)估计袋中白球的个数．

    (1)0.25(2)估计袋中有3个白球 【解析】试题分析：（1）用大量重复试验中事件发生的频率稳定到某个常数来表示该事件发生的概率即可； （2）列用概率公式列出方程求解即可； 试题解析：（1）251÷1000=0.251； ∵大量重复试验事件发生的频率逐渐稳定到0.25附近， ∴估计从袋中摸出一个球是黑球的概率是0.25； （2）设袋中白球为x个， =0....

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学人教版上册 全册综合测试卷 题型：单选题

    如图，在△ABC中，∠C＝40°，将△ABC沿着直线l折叠，点C落在点D的位置，则∠1－∠2的度数是（ ）

    A. 40° B. 80° C. 90° D. 140°

    B 【解析】 由题意得：∠C=∠D， ∵∠1=∠C+∠3，∠3=∠2+∠D， ∴∠1=∠2+∠C+∠D=∠2+2∠C， ∴∠1－∠2=2∠C=80°. 故选B.

    查看答案和解析>>

    科目：初中数学 来源：湖南邵阳市区2017-2018学年八年级上册数学期末试卷 题型：填空题

    不等式 的解集是 _____________。

    x>-1 【解析】, +3, .

    查看答案和解析>>

    科目：初中数学 来源：湖南邵阳市区2017-2018学年八年级上册数学期末试卷 题型：单选题

    估计的值 （ ）

    A. 在1和2之间 B. 在2和3之间 C. 在3和4之间 D. 在4和5之间

    C 【解析】∵， ∴， 故选C.

    查看答案和解析>>

    科目：初中数学 来源：2018人教版八年级数学下册练习：第十七章达标检测卷 题型：解答题

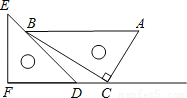
    一副直角三角板如图放置，点C在FD的延长线上，AB∥CF，∠F=∠ACB=90°，∠E=45°，∠A=60°，AC=10，试求CD的长．

    15﹣5． 【解析】 试题分析：过点B作BM⊥FD于点M，根据题意可求出BC的长度，然后在△EFD中可求出∠EDF=45°，进而可得出答案． 【解析】 过点B作BM⊥FD于点M， 在△ACB中，∠ACB=90°，∠A=60°，AC=10， ∴∠ABC=30°，BC=AC×tan60°=10， ∵AB∥CF， ∴BM=BC×sin30°=10×=5， ...

    查看答案和解析>>

    科目：初中数学 来源：2018人教版八年级数学下册练习：第十七章达标检测卷 题型：单选题

    如图，将长方形纸片ABCD折叠，使边DC落在对角线AC上，折痕为CE，且D点落在对角线上D'处.若AB=3，AD=4，则ED的长为(　　)

    A. B. 3 C. 1 D.

    A 【解析】首先利用勾股定理计算出AC的长，再根据折叠可得△DEC≌△D′EC，设ED=x，则D′E=x，AD′=AC﹣CD′=2，AE=4﹣x，再根据勾股定理可得方程22+x2=（4﹣x）2，再解方程即可． 【解析】 ∵AB=3，AD=4， ∴DC=3， ∴AC==5， 根据折叠可得：△DEC≌△D′EC， ∴D′C=DC=3，DE=D′E， 设ED=...

    查看答案和解析>>

    科目：初中数学 来源：湖北省襄阳老河口市2018届九年级上学期期末考试数学试卷 题型：解答题

    如图，在△ABC中，正方形EDCF的三个顶点E，D，F都在三角形的边上，另一个顶点C与三角形的顶点重合，且AC=4，BC=6，求ED的长．

    【解析】试题分析：先根据两角对应相等的两三角形相似证得△AED∽△ABC，然后根据相似三角形的对应边成比例，可求解. 试题解析：∵四边形EDCF是正方形， ∴ED=DC，∠EDA =∠EDC =∠C =90° 又∵∠A =∠A，∴△AED∽△ABC. ∴，即ED·AC=BC·AD. ∵AC=4，BC=6，AC=AD+CD，∴4ED=6(4-ED), 解得 ...

    查看答案和解析>>

    科目：初中数学 来源：山西省吕梁市孝义市2016-2017学年九年级（上）期末考试数学试卷 题型：解答题

    综合与探究

    如图，在平面直角坐标系xOy中，抛物线W的函数表达式为y=﹣x2+2x+3，抛物线W与x轴交于A、B两点（点A在点B的右侧），与y轴交于点C，它的顶点为D，直线l经过A、C两点．

    （1）求点A、B、C、D的坐标．

    （2）将直线l向下平移m个单位，对应的直线为l′．

    ①若直线l′与x轴的正半轴交于点E，与y轴的正半轴交于点F，△AEF的面积为S，求S关于m的函数关系式，并写出自变量m的取值范围；

    ②求m的值为多少时，S的值最大？最大值为多少？

    （3）若将抛物线W也向下平移m单位，再向右平移1个单位，使平移后得到的二次函数图象的顶点P落在△AOC的内部（不包括△AOC的边界），请直接写出m的取值范围．

    （1）点D坐标为（1，4）（2）①S=﹣m2+m（0＜m＜3），②当m=时，S的值最大，最大值为（3）3＜m＜4 【解析】试题分析：（1）令y＝0，求出A，B的横坐标，令x＝0求出C的纵坐标，把二次函数解析式转化为顶点式即可得出D的坐标； （2）①利用待定系数法确定出直线l的解析式，根据平移得出l′的解析式，求出与坐标轴的交点E，F的坐标，得出AE，OF的长，最后用面积公式即可得出结论...

    查看答案和解析>>

    同步练习册答案