
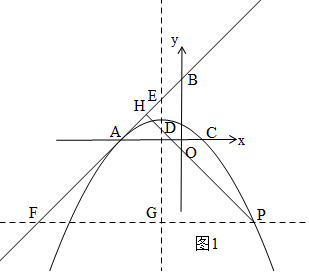
 ��ͼ��������y=-$\frac{1}{4}$x2-$\frac{1}{2}$x+$\frac{3}{4}$��x�ύ��A��C���㣨��A�ڵ�C����ߣ���ֱ��y=kx+b��k��0���ֱ�x�ᣬy����A��B���㣬�ҳ��˵�A֮�⣬��ֱ����������û�������κν��㣮
��ͼ��������y=-$\frac{1}{4}$x2-$\frac{1}{2}$x+$\frac{3}{4}$��x�ύ��A��C���㣨��A�ڵ�C����ߣ���ֱ��y=kx+b��k��0���ֱ�x�ᣬy����A��B���㣬�ҳ��˵�A֮�⣬��ֱ����������û�������κν��㣮���� ��1����y=0���������ߵĽ���ʽ���ⷽ�̿ɵ�A��C�����ꣻ
��2����A����������ֱ�߽���ʽ�еã�b=3k���ɸ�ֱ����������ֻ��һ������ã������ߺ�ֱ�ߵĽ���ʽ�з����飬��=0���ɵ�k��ֵ���Ӷ�����b��ֵ��
��3����P��x���ƽ���߽�ֱ��AB��F�����Գ�����G�����ݡ�AOB�ǵ���ֱ�������οɵã�PH+DH=HF+HE=EF=$\sqrt{2}$EG��Ҳ����PH+DH����Сֵ������ȡ����EG�ij��̣���G�������ߵĶ���ʱ��EG��СΪ1���ɵý��ۣ�
���  �⣺��1��y=-$\frac{1}{4}$x2-$\frac{1}{2}$x+$\frac{3}{4}$��
�⣺��1��y=-$\frac{1}{4}$x2-$\frac{1}{2}$x+$\frac{3}{4}$��
��y=0ʱ��-$\frac{1}{4}$x2-$\frac{1}{2}$x+$\frac{3}{4}$=0��
x2+2x-3=0��
��x+3����x-1��=0��
x=-3��1��
�ߵ�A�ڵ�C����ߣ�
��A��-3��0����C��1��0����
��2����A��-3��0������y=kx+b�еã�-3k+b=0��
b=3k��
��ֱ��AB����ʽΪ��y=kx+3k��
��$\left\{\begin{array}{l}{y=kx+3k}\\{y=-\frac{1}{4}{x}^{2}-\frac{1}{2}x+\frac{3}{4}}\end{array}\right.$��
-$\frac{1}{4}{x}^{2}$-$\frac{1}{2}$x+$\frac{3}{4}$=kx+3k��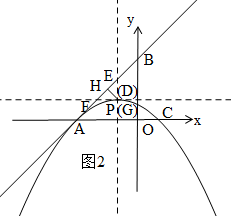
x2+��4k+2��x+12k-3=0��
��=��4k+2��2-4��12k-3��=0��
k=1��
��ֱ��AB����ʽΪ��y=x+3��
��B��0��3����
��k=1��b=3��
��3����ͼ1���Գ��x=-$\frac{-\frac{1}{2}}{2����-\frac{1}{4}��}$=-1��
��Գ�����ֱ��AB�Ľ���E��-1��2����
��P��x���ƽ���߽�ֱ��AB��F�����Գ�����G��
��OA=OB=3����AOB=90�㣬
���AOB�ǵ���ֱ�������Σ�
���ABO=��BAO=45�㣬
��PH=HF��DH=HE��
��PH+DH=HF+HE=EF=$\sqrt{2}$EG��
��EG��Сʱ��PH+DH����Сֵ��
����ͼ2����G��P��D�����غϣ�λ�������ߵĶ��㣨-1��1��ʱ��EG��С=2-1=1��
��PH+DH����Сֵ=$\sqrt{2}$��
���� ���⿼���˺�����������Ľ��㡢����ͼ���ϵ�����������ʽ�е���ĸϵ���������뷽�����Ĺ�ϵ���߶κ͵���ֵ���⣬���������Ѷȣ�ȷ����ֵʱ��P��λ���ǹؼ���


 ��ѧ����ͬ����ϰϵ�д�
��ѧ����ͬ����ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
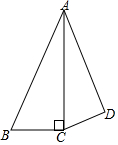 ��ͼ��AC�ǡ�BAD��ƽ���ߣ�BC��AC��CD��AD����AB=4��AD=$\frac{9}{4}$����AC�ij�Ϊ3��
��ͼ��AC�ǡ�BAD��ƽ���ߣ�BC��AC��CD��AD����AB=4��AD=$\frac{9}{4}$����AC�ij�Ϊ3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com