
【题目】材料一:一个正整数x能写成x=a2﹣b2(a,b均为正整数,且a≠b),则称x为“雪松数”,a,b为x的一个平方差分解,在x的所有平方差分解中,若a2+b2最大,则称a,b为x的最佳平方差分解,此时F(x)=a2+b2.
例如:24=72﹣52,24为雪松数,7和5为24的一个平方差分解,32=92﹣72,32=62﹣22,因为92+72>62+22,所以9和7为32的最佳平方差分解,F(32)=92+72
材料二:若一个四位正整数,它的千位数字与个位数字相同,百位数字与十位数字相同,但四个数字不全相同,则称这个四位数为“南麓数”.例如4334,5665均为“南麓数”.
根据材料回答:
(1)请直接写出两个雪松数,并分别写出它们的一对平方差分解;
(2)试证明10不是雪松数;
(3)若一个数t既是“雪松数”又是“南麓数”,并且另一个“南麓数”的前两位数字组成的两位数与后两位数字组成的两位数恰好是t的一个平方差分解,请求出所有满足条件的数t中F(t)的最大值.
【答案】(1)112=112﹣32,40=72﹣32;(2)见解析;(3)12020.
【解析】试题分析:(1)根据雪松数的特征即可得到结论;
(2)根据题意即可得到结论;
(3)设t=![]() (a,b均为正整数,且0<a≠b≤9),另一个“南麓数”为t′=
(a,b均为正整数,且0<a≠b≤9),另一个“南麓数”为t′=![]() (m,n均为正整数,且0<n<m≤9),根据“南麓数”的特征即可得到结论.
(m,n均为正整数,且0<n<m≤9),根据“南麓数”的特征即可得到结论.
试题解析:解:(1)112=112﹣32,40=72﹣32;
(2)若10是“雪松数”,则可设a2﹣b2=10(a,b均为正整数,且a≠b),则(a+b)(a﹣b)=10.又∵10=2×5=10×1.∵a,b均为正整数,∴a+b>a﹣b,∴![]() ,或
,或![]() ,解得:
,解得:![]() 或
或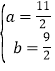 ,与a,b均为正整数矛盾,故10不是雪松数;
,与a,b均为正整数矛盾,故10不是雪松数;
(3)设t=![]() (a,b均为正整数,且0<a≠b≤9),另一个“南麓数”为t′=
(a,b均为正整数,且0<a≠b≤9),另一个“南麓数”为t′=![]() (m,n均为正整数,且0<n<m≤9),则t=(10m+n)2﹣(10n+m)2=99(m2﹣n2)=99(m+n)(m﹣n),∴99(m+n)(m﹣n)=1000a+100b+10b+a=1001a+110b,整理得,(m+n)(m﹣n)=10a+b+
(m,n均为正整数,且0<n<m≤9),则t=(10m+n)2﹣(10n+m)2=99(m2﹣n2)=99(m+n)(m﹣n),∴99(m+n)(m﹣n)=1000a+100b+10b+a=1001a+110b,整理得,(m+n)(m﹣n)=10a+b+![]() .∵a,b,m,n均为正整数,∴a+b=9,经探究
.∵a,b,m,n均为正整数,∴a+b=9,经探究![]() ,符合题意,∴t的值分别为:2772,5445,t′的值分别为:8668,8338,由材料一可知,F(t)的最大值为:862+682=12020.
,符合题意,∴t的值分别为:2772,5445,t′的值分别为:8668,8338,由材料一可知,F(t)的最大值为:862+682=12020.


科目:初中数学 来源: 题型:
【题目】已知:二次函数y=x2+bx+c的图象与x轴交于A,B两点,其中A点坐标为(﹣3,0),与y轴交于点C,点D(﹣2,﹣3)在抛物线上. 
(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,求出PA+PD的最小值;
(3)若抛物线上有一动点P,使三角形ABP的面积为6,求P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】结合数轴与绝对值的知识回答下列问题:
(1)探究:
①数轴上表示5和2的两点之间的距离是多少.
②数轴上表示﹣2和﹣6的两点之间的距离是多少.
③数轴上表示﹣4和3的两点之间的距离是多少.
(2)归纳:
一般的,数轴上表示数m和数n的两点之间的距离等于|m﹣n|.
(3)应用:
①如果表示数a和3的两点之间的距离是7,则可记为:|a﹣3|=7,求a的值.
②若数轴上表示数a的点位于﹣4与3之间,求|a+4|+|a﹣3|的值.
![]()
③当a取何值时,|a+4|+|a﹣1|+|a﹣3|的值最小,最小值是多少?请说明理由.
![]()
(4)拓展:某一直线沿街有2014户居民(相邻两户居民间隔相同):A1,A2,A3,A4,A5,…A2014,某餐饮公司想为这2014户居民提供早餐,决定在路旁建立一个快餐店P,点P选在什么线段上,才能使这2014户居民到点P的距离总和最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习有理数运算时发现以下三个等式:(ab)2=a2b2,(ab)3=a3b3,(ab)4=a4b4.
(1)他把a=﹣2,b=3代入到第一个等式的左右两边验证:
因为,左=(﹣2×3)2=36,右=(﹣2)2×32=36,左=右,所以成立.
请你帮他把a=﹣2,b=3代入到后两个等式的左右两边验证是否成立;
(2)通过上述验证,请你猜想直接写出结果:(ab)365等于多少,归纳得出:(ab)n等于多少(n为正整数);
(3)请应用(2)中归出的结论计算:(﹣![]() )2017×112018
)2017×112018
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,![]() ,
,![]() 的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,
的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,![]() ,垂足为G,若
,垂足为G,若![]() ,则AE的边长为
,则AE的边长为![]()
![]()

A. ![]() B.
B. ![]() C. 4 D. 8
C. 4 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是正△ABC内的一点,且PA=6,PB=8,PC=10.若将△PAC绕点A逆时针旋转后,得到△P′AB. 
(1)求旋转角的度数;
(2)求点P与点P′之间的距离;
(3)求∠APB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠B,∠C的平分线交于点O,D是外角与内角平分线交点,E是外角平分线交点,若∠BOC=120°,则∠D=( )

A. 15° B. 20° C. 25° D. 30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若两个二次函数图象的顶点、开口方向都相同,则称这两个二次函数为“同簇二次函数”.
(1)请写出两个为“同簇二次函数”的函数;
(2)已知关于x的二次函数y1=2x2﹣4mx+2m2+1和y2=ax2+bx+5,其中y1的图象经过点A(1,1),若y1+y2与y1为“同簇二次函数”,求函数y2的表达式,并求出当0≤x≤3时,y2的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com