
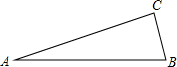
 (2011•南宁)如图,在△ABC中,∠ACB=90°,∠A=15°,AB=8,则AC•BC的值为( )
(2011•南宁)如图,在△ABC中,∠ACB=90°,∠A=15°,AB=8,则AC•BC的值为( )| 1 |
| 2 |
| BC |
| AB |
| AC |
| AB |
| 1 |
| 2 |

| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
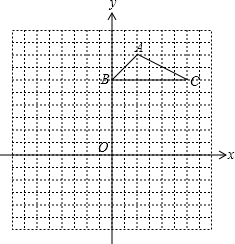 (2011•南宁)如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立平面直角坐标系.
(2011•南宁)如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立平面直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:
 于点B.
于点B.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2011•南宁)如图,在圆锥形的稻草堆顶点P处有一只猫,看到底面圆周上的点A处有一只老鼠,猫沿着母线PA下去抓老鼠,猫到达点A时,老鼠已沿着底面圆周逃跑,猫在后面沿着相同的路线追,在圆周的点B处抓到了老鼠后沿母线BP回到顶点P处.在这个过程中,假设猫的速度是匀速的,猫出发后与点P距离s,所用时间为t,则s与t之间的函数关系图象是( )
(2011•南宁)如图,在圆锥形的稻草堆顶点P处有一只猫,看到底面圆周上的点A处有一只老鼠,猫沿着母线PA下去抓老鼠,猫到达点A时,老鼠已沿着底面圆周逃跑,猫在后面沿着相同的路线追,在圆周的点B处抓到了老鼠后沿母线BP回到顶点P处.在这个过程中,假设猫的速度是匀速的,猫出发后与点P距离s,所用时间为t,则s与t之间的函数关系图象是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com