
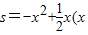 >0),利用函数的图象或通过配方均可求得该函数的最大值.
>0),利用函数的图象或通过配方均可求得该函数的最大值.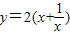 (x>0),问题就转化为研究该函数的最大(小)值了.
(x>0),问题就转化为研究该函数的最大(小)值了.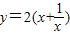 (x>0)的最大(小)值.
(x>0)的最大(小)值.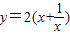 (x>0)的图象:
(x>0)的图象:| x | … |  |  |  | 1 | 2 | 3 | 4 | … |
| y | … | … |
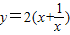 (x>0)有最______值(填“大”或“小”),是______.
(x>0)有最______值(填“大”或“小”),是______.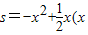 >0)的最大值,请你尝试通过配方求函数
>0)的最大值,请你尝试通过配方求函数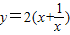 (x>0)的最大(小)值,以证明你的猜想.〔提示:当x>0时,
(x>0)的最大(小)值,以证明你的猜想.〔提示:当x>0时,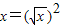 〕
〕
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
 s,则s与x的函数关系式为:s=-x2+
s,则s与x的函数关系式为:s=-x2+| 1 |
| 2 |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| x | … |
|
|
|
1 | 2 | 3 | 4 | … | ||||||
| y | … | … |
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| x |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 的圆孔,需对铁片进行处理(规定铁片与圆孔有接触时铁片不能穿过圆孔);
的圆孔,需对铁片进行处理(规定铁片与圆孔有接触时铁片不能穿过圆孔);


 时,判断直角梯形铁片EBAF能否穿过圆孔,并说明理由;
时,判断直角梯形铁片EBAF能否穿过圆孔,并说明理由; 查看答案和解析>>
科目:初中数学 来源:2012届江苏省江阴市石庄中学九年级中考模拟考试数学试卷(带解析) 题型:解答题
问题背景:
如图1,矩形铁片ABCD的长为2a,宽为a; 为了要让铁片能穿过直径为 的圆孔,需对铁片进行处理(规定铁片与圆孔有接触时铁片不能穿过圆孔);
的圆孔,需对铁片进行处理(规定铁片与圆孔有接触时铁片不能穿过圆孔);
探究发现:
【小题1】如图2,M、N、P、Q分别是AD、AB、BC、CD的中点,若将矩形铁片的四个角去掉,只余下四边形MNPQ,则此时铁片的形状是 _______,给出证明,并通过计算说明此时铁片都能穿过圆孔;
拓展迁移:
【小题2】如图3,过矩形铁片ABCD的中心作一条直线分别交边BC、AD于点E、F(不与端点重合),沿着这条直线将矩形 铁片切割成两个全等的直角梯形铁片;
①当BE=DF= 时,判断直角梯形铁片EBAF能否穿过圆孔,并说明理由;
时,判断直角梯形铁片EBAF能否穿过圆孔,并说明理由;
②为了能使直角梯形铁片EBAF顺利穿过圆孔,请直接写出线段BE的长度的取值范围 .
查看答案和解析>>
科目:初中数学 来源:2012-2013学年浙江省杭州市萧山区金山中学九年级(上)月考数学试卷(10月份)(解析版) 题型:解答题
 >0),利用函数的图象或通过配方均可求得该函数的最大值.
>0),利用函数的图象或通过配方均可求得该函数的最大值. (x>0),问题就转化为研究该函数的最大(小)值了.
(x>0),问题就转化为研究该函数的最大(小)值了. (x>0)的最大(小)值.
(x>0)的最大(小)值. (x>0)的图象:
(x>0)的图象:| x | … |  |  |  | 1 | 2 | 3 | 4 | … |
| y | … | … |
 (x>0)有最______值(填“大”或“小”),是______.
(x>0)有最______值(填“大”或“小”),是______. >0)的最大值,请你尝试通过配方求函数
>0)的最大值,请你尝试通过配方求函数 (x>0)的最大(小)值,以证明你的猜想.〔提示:当x>0时,
(x>0)的最大(小)值,以证明你的猜想.〔提示:当x>0时, 〕
〕
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com