
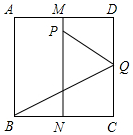
 如图,面积为1的正方形ABCD中,M,N分别为AD、BC的中点,将C点折至MN上,落在P点的位置,折痕为BQ,连接PQ.以PQ为边长的正方形的面积等于$\frac{1}{3}$.
如图,面积为1的正方形ABCD中,M,N分别为AD、BC的中点,将C点折至MN上,落在P点的位置,折痕为BQ,连接PQ.以PQ为边长的正方形的面积等于$\frac{1}{3}$. 分析 根据折叠的性质,可得PQ=QC,∠PBQ=∠QBC=30°;再在Rt△BCQ中,根据三角函数的定义可求得PQ的值,进而可得答案.
解答 解:由折法知PQ=QC,∠PBQ=∠QBC=30°.
在Rt△BCQ中,QC=BC•tan30°=1×$\frac{\sqrt{3}}{3}$=$\frac{\sqrt{3}}{3}$,
∴PQ=$\frac{\sqrt{3}}{3}$.
∴以PQ为边的正方形的面积为$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 考查了正方形的性质,翻折变换(折叠问题),解答本题要充分利用正方形的特殊性质.注意在正方形中的特殊三角形的应用,搞清楚矩形、菱形、正方形中的三角形的三边关系,可有助于提高解题速度和准确率.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
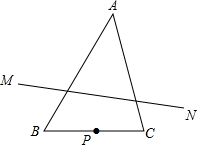 如图,在△ABC中,∠A=45°,∠B=60°,AB=4,P是BC边上的动点(不与B,C重合),点P关于直线AB,AC的对称点分别为M,N,则线段MN长的取值范围是2$\sqrt{6}$≤MN<4$\sqrt{2}$.
如图,在△ABC中,∠A=45°,∠B=60°,AB=4,P是BC边上的动点(不与B,C重合),点P关于直线AB,AC的对称点分别为M,N,则线段MN长的取值范围是2$\sqrt{6}$≤MN<4$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在矩形ABCD中,AB=$\sqrt{2}$,AD=2,以点A为圆心,AD的长为半径的圆交BC边于点E,则图中阴影部分的面积为( )
如图,在矩形ABCD中,AB=$\sqrt{2}$,AD=2,以点A为圆心,AD的长为半径的圆交BC边于点E,则图中阴影部分的面积为( )| A. | $2\sqrt{2}-1-\frac{π}{3}$ | B. | $2\sqrt{2}-1-\frac{π}{2}$ | C. | $2\sqrt{2}-2-\frac{π}{2}$ | D. | $2\sqrt{2}-1-\frac{π}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9.93×108 | B. | 9.93×109 | C. | 99.3×109 | D. | 9.93×107 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com