
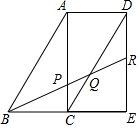
 取三个完全相同的三角板拼成如图所示的形状,R为DE的中点,BR分别交AC,CD于P,Q,则BP:PQ:QR=( )
取三个完全相同的三角板拼成如图所示的形状,R为DE的中点,BR分别交AC,CD于P,Q,则BP:PQ:QR=( )| A. | 3:1:2 | B. | 5:2:3 | C. | 4:1:3 | D. | 6:1:3 |
分析 利用根据三角形全等结合平行四边形的性质得到平行,可得到PB=PR,$\frac{PC}{RE}$=$\frac{1}{2}$,且DR=RE,代入可得到QR和PQ之间的关系,结合BP=PR=3PQ,可得到答案.
解答 解:∵三个三角形是全等三角形,
∴BC=AD=CE,AC∥DE,
∴$\frac{BP}{PR}$=$\frac{BC}{CE}$=1,∴BC=AD=CE,AC∥DE,
∴PB=PR,$\frac{PC}{RE}$=$\frac{1}{2}$,
又∵PC∥DR,
∴△PCQ∽△RDQ,
又∵点R是DE中点,
∴DR=RE,
∴$\frac{PQ}{QR}$=$\frac{PC}{DR}$=$\frac{PC}{RE}$=$\frac{1}{2}$,
∴QR=2PQ,
又∵BP=PR=PQ+QR=3PQ,
∴BP:PQ:QR=3:1:2,
故选:A.
点评 本题主要考查平行线分线段成比例的性质及平行四边形的性质,由条件得到QR=2PQ、BP=3PQ是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 要给一个长、宽、高分别为x,y,z的箱子打包,其打包方式如图所示.
要给一个长、宽、高分别为x,y,z的箱子打包,其打包方式如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
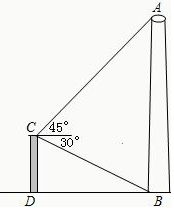 如图,在城市改造时,要拆除建筑物AB,在离它21米远的建筑物CD顶端C测得A的仰角45°,B的俯角30°,在点B的35米处有一文物,问:此文物是否在危险区内?请说明理由.(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,在城市改造时,要拆除建筑物AB,在离它21米远的建筑物CD顶端C测得A的仰角45°,B的俯角30°,在点B的35米处有一文物,问:此文物是否在危险区内?请说明理由.(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com