
| A. | $\frac{1}{3}$、$\frac{1}{4}$、$\frac{1}{5}$ | B. | 1、2、$\sqrt{3}$ | C. | 5、12、13 | D. | 6、10、8 |
分析 根据勾股定理的逆定理进行判断.
解答 解:A、因为$(\frac{1}{3})^{2}+(\frac{1}{4})^{2}$=$\frac{25}{144}$,$(\frac{1}{5})^{2}$=$\frac{1}{25}$,所以$(\frac{1}{3})^{2}+(\frac{1}{4})^{2}$≠$(\frac{1}{5})^{2}$,故选项A不能构成直角三角形;
B、因为12+$(\sqrt{3})^{2}$=22,所以选项B能构成直角三角形;
C、因为52+122=132,所以选项C能构成直角三角形;
D、因为62+82=102,所以选项D能构成直角三角形;
故选A.
点评 本题考查了勾股定理的逆定理,分别计算两条较小边的平方和,与大边的平方比较,相等则能构成直角三角形,反之则不能.


 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
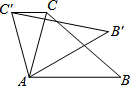 如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=( )
如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=( )| A. | 30° | B. | 35° | C. | 40° | D. | 50° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a、b两数的平方和 | |
| B. | a与b的和的平方 | |
| C. | a2与b2的和 | |
| D. | 边长为a的正方形与边长为b的正方形的面积和 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com