练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．四个数3，-2，0，-|-4|中，其中比零小的数的个数是（　　）
    A．1B．2C．3D．4

    分析 根据有理数大小比较的法则：①正数都大于0；②负数都小于0；③正数大于一切负数；④两个负数，绝对值大的其值反而小，判断出四个数3，-2，0，-|-4|中，其中比零小的数的个数是多少即可．

    解答 解：∵3＞0，-2＜0，-|-4|=-4＜0，
    ∴四个数3，-2，0，-|-4|中，其中比零小的数有2个：
    -2，-|-4|．
    故选：B．

    点评 此题主要考查了有理数大小比较的方法，要熟练掌握，解答此题的关键是要明确：①正数都大于0；②负数都小于0；③正数大于一切负数；④两个负数，绝对值大的其值反而小．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    11．下列分数中，能化为有限小数的是（　　）
    A．$\frac{1}{8}$B．$\frac{1}{9}$C．$\frac{1}{12}$D．$\frac{1}{15}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．下列说法正确的个数为（　　）个
    ①两组对边分别相等的四边形是平行四边形
    ②对角线相等的四边形是矩形
    ③对角线互相垂直的平行四边形是菱形
    ④正方形是轴对称图形，有2条对称轴．
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

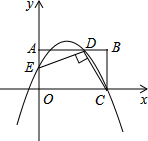    9．如图，平面直角坐标系xOy中，矩形OABC的边OA在y轴的正半轴上，OC在x轴的正半轴上，OA=2，OC=3，AD=2，连接DC，过点D作DE⊥DC交OA于点E．
    （1）直接写出E的坐标（0，1）；
    （2）求过E、D、C三点的抛物线解析式；
    （3）将∠EDC绕点D顺时针旋转后，角的一边与y轴的正半轴交于点F，另一边与线段OC交于点G，在旋转的过程中，直线DF与抛物线的另一交点为M，且M的横坐标为1.2那么EF=2GO成立吗？为什么？
    （4）对于（3）中的G点，在位于第一象限的抛物线上是否存在点Q，使得直线GQ与AB的交点P与点C、G构成等腰△PCG？若存在，求出Q的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．如图，△ABC绕旋转中心（-1，0）旋转180°得到△A′B′C′，如果△ABC上的点P的坐标为（a，b），那么它的对应点P′的坐标为（　　）
    A．（a-2，b）B．（a+2，b）C．（-a-2，-b）D．（a+2，-b）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．下列式子没有意义的是（　　）
    A．$\sqrt{-2}$B．$\sqrt{0}$C．$\sqrt{-（-2）}$D．$\sqrt{（-1）^{2}}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

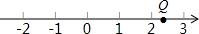    13．如图，数轴上的点Q所表示的数可能是（　　）
    A．$\sqrt{2}$B．$\sqrt{3}$C．$\sqrt{5}$D．$\sqrt{10}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．下列各组数中互为相反数的是（　　）
    A．2 与-$\frac{1}{2}$B．-2与2C．2 与丨-2|D．$\frac{1}{2}$与-2

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

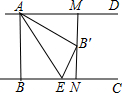    11．如图，已知AD∥BC，AB⊥BC，AB=3，点E为射线BC上一个动点，连接AE，将△ABE沿AE折叠，点B落在点B′处，过点B′作AD的垂线，分别交AD，BC于点M，N．当点B′为线段MN的三等分点时，BE的长为$\frac{3\sqrt{2}}{2}$或$\frac{3\sqrt{5}}{5}$．

    查看答案和解析>>

    同步练习册答案