
【题目】如图,已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,把线段
,把线段![]() 沿射线
沿射线![]() 方向平移至
方向平移至![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,又联结
,又联结![]() 与直线
与直线![]() 交于点
交于点![]() .
.
(1)若![]() ,求
,求![]() 的长;
的长;
(2)设![]() ,
,![]() ,试求
,试求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)当![]() 为多少时,以
为多少时,以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?
相似?
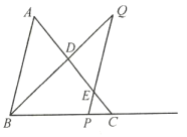
【答案】(1)![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 为4时,以
为4时,以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似.
相似.
【解析】
(1)首先判定四边形![]() 是平行四边形,然后得出
是平行四边形,然后得出![]() ,再有比例关系列出等式即可得解;
,再有比例关系列出等式即可得解;
(2)首先由平行的性质得出比例关系的等式,然后分类讨论P点,代入数据,即可得解;
(3)首先由平行的性质得出![]() ,又以
,又以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,得出
相似,得出![]() 与
与![]() 相似,进而列出等式,即可得解.
相似,进而列出等式,即可得解.
(1)联结![]() .
.
![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() ,
,![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
(2)![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
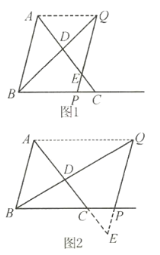
当点![]() 在边
在边![]() 上时(如图1),
上时(如图1),
![]() ,解得
,解得![]() ,
,
![]() ,解得
,解得![]() ,
,
![]() .
.
当点![]() 在边
在边![]() 的延长线上时(如图2),
的延长线上时(如图2),
![]() ,解得
,解得![]() ,
,
![]() ,解得
,解得![]() ,
,
![]()
![]() ,
,
综上所述,![]() .
.
(3)![]() ,
,
![]() ,
,
又以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,
相似,
![]() 与
与![]() 相似,
相似,
![]() 公共,
公共,
又![]() ,
,
![]() ,
,
![]() ,即
,即![]() ,
,
由(2)知,![]() ,
,
![]() ,得
,得![]() ,
,
所以,当![]() 为4时,以
为4时,以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似.
相似.


科目:初中数学 来源: 题型:
【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边由长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
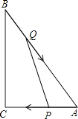
【题目】.如图,在RT△ABC中,∠C=90°,BC=8,AC=6,动点Q从B点开始在线段BA上以每秒2个单位长度的速度向点A移动,同时点P从A点开始在线段AC上以每秒1个单位长度的速度向点C移动.当一点停止运动,另一点也随之停止运动.设点Q,P移动的时间为t秒.当t=____________ 秒时△APQ与△ABC相似.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某空调生产厂的装配车间计划在一段时期内组装9000台空调,设每天组装的空调数量为y(台/天),组装的时间为x(天).
(1)直接写出y与x之间的函数关系式;
(2)原计划用60天完成这一任务,但由于气温提前升高,厂家决定这批空调至少要提前10天完成,那么装配车间每天至少要组装多少台空调?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC是等边三角形,点D、E分别在边BC、AC上,且BD=CE,AD与BE相交于点F.
(1)求证:△ABD≌△BCE
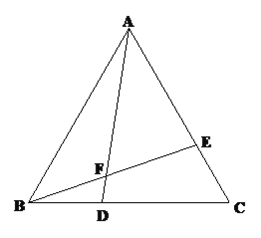
(2)求证: ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“特色大丰,美好生活”, 大丰区举行金色秋天旅游活动.明明和华华同学分析网上关于旅游活动的信息,发现最具特色的景点有:①荷兰花海、②梅花弯、③麋鹿保护区.他们准备周日下午去参观游览,各自在这三个景点任选一个,每个景点被选中的可能性相同.
(1)明明同学在三个备选景点中选中荷兰花海的概率是 .
(2)用树状图或列表法求出明明和华华他们选中不同景点参观的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程mx2+(3﹣m)x﹣3=0(m为实数,m≠0).
(1) 试说明:此方程总有两个实数根.
(2) 如果此方程的两个实数根都为正整数,求整数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC⊥BD垂足为点E,点F,M分别是AB,BC的中点,BN平分∠ABE交AM于点N,AB=AC=BD,连接NF.
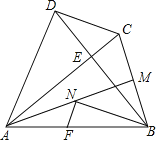
(1)判断线段MN与线段BM的位置关系与数量关系,说明理由;
(2)如果CD=5,求NF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】P是△ABC一边上的一点(P不与A、B、C重合),过点P的一条直线截△ABC,如果截得的三角形与△ABC相似,我们称这条直线为过点P的△ABC的“相似线”.Rt△ABC中,∠C=90°,∠A=30°,当点P为AC的中点时,过点P的△ABC的“相似线”最多有几条?( )
A. 1条B. 2条C. 3条D. 4条
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com