
【题目】如图,点C为线段AD上一点,B为CD的中点,且AD=10cm,BD=4cm;
(1)图中共有多少条线段?写出这些线段;
(2)求AC的长;
(3)若点E在直线AD上,且AE=3cm,求BE的长;
![]()
【答案】(1)6条,线段AC,AB,AD,CB,CD,BD;(2)2cm;(3)BE=3cm或9cm;
【解析】
(1)根据直线上线段的条数公式:直线上有n个点,线段的条数是![]() ,可得答案;
,可得答案;
(2)根据线段中点的性质,可用BC表示CD,根据线段的和差,可得关于BC的方程,根据解方程,可得BC的长,AC的长;
(3)分类讨论:点E在线段AD上,点E在线段AD的延长线上,根据线段的和差,可得答案.
(1)图中共有6条线段,分别是:线段AC,AB,AD,CB,CD,BD;
(2)∵BD=4cm,B为CD的中点,
∴CD=2 BD=2×4=8(cm)
又∵AD=10 ∴ AC=AD-CD=10-8=2(cm)
(3)点E在直线AD上有两种情况:
①E在线段AD上,如图,
∵ AB=AD-BD=10-4=6
∴ BE= AB-AE=6-3=3(cm)
②E在线段DA的延长线上,如图的点E′,
由①知:AB=6
∴ BE′= AB+AE′=6+3=9(cm)
综上可得: BE=3cm或9cm;


科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=10,AC=2![]() ,BC边上的高AD=6,则另一边BC等于_______.
,BC边上的高AD=6,则另一边BC等于_______.
【答案】10或6
【解析】试题解析:根据题意画出图形,如图所示,

如图1所示,AB=10,AC=2![]() ,AD=6,
,AD=6,
在Rt△ABD和Rt△ACD中,
根据勾股定理得:BD=![]() =8,CD=
=8,CD=![]() =2,
=2,
此时BC=BD+CD=8+2=10;
如图2所示,AB=10,AC=2![]() ,AD=6,
,AD=6,
在Rt△ABD和Rt△ACD中,
根据勾股定理得:BD=![]() =8,CD=
=8,CD=![]() =2,
=2,
此时BC=BD-CD=8-2=6,
则BC的长为6或10.
【题型】填空题
【结束】
12
【题目】在平面直角坐标系中,已知一次函数y=2x+1的图象经过P1(x1,y1)、P2(x2,y2)两点,若x1<x2,则y1 ______ y2.(填“>”“<”或“=”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是给定△ABC边AB上一动点,D是CP的延长线上一点,且2DP=PC,连结DB,动点P从点B出发,沿BA方向匀速运动到终点A,则△APC与△DBP面积的差的变化情况是( )
A.始终不变
B.先减小后增大
C.一直变大
D.一直变小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D′处.若AB=3,AD=4,则ED的长为( )

A. ![]() B. 3 C. 1 D.
B. 3 C. 1 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B的坐标分别为(0,8),(﹣3,0),点P从点A出发,以2单位/秒的速度沿射线AO方向运动,同时点E从点B出发,以1单位/秒的速度沿射线BO方向运动,以PE为斜边构造Rt△PEC(字母按逆时针顺序),且EC=2PC,抛物线y=﹣2x2+bx+c经过点(0,4),(﹣1,﹣2),设运动时间为t秒.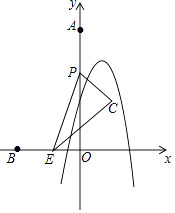
(1)求该抛物线的表达式;
(2)当t=2时,求点C的坐标;
(3)①当t<3时,求点C的坐标(用含t的代数式表示);
②在运动过程中,若点C恰好落在该抛物线上,请直接写出所有满足条件的t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形城池ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E、南门点F分别是AB,AD的中点,EG⊥AB,FH⊥AD,EG=15里,HG经过A点,则FH=里. 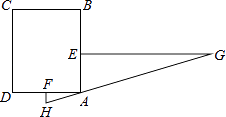
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在方格纸中,已知格点△ABC和格点O.
(1)画出△ABC关于点O对称的△A′B′C′;
(2)若以点A、O、C、D为顶点的四边形是平行四边形,则点D的坐标为__.(写出所有可能的结果)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为1cm的等边三角形ABC沿直线l向右翻动(不滑动),点B从开始到结束,所经过路径的长度为( ) 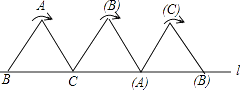
A.![]() cm
cm
B.(2+ ![]() π)cm
π)cm
C.![]() cm
cm
D.3cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com