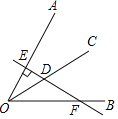
【题目】已知∠AOB＝60°，OC是∠AOB的平分线，点D为OC上一点，过D作直线DE⊥OA，垂足为点E，且直线DE交OB于点F，如图所示．若DE＝2，则DF＝_____．
优等生题库系列答案
53天天练系列答案科目：初中数学 来源： 题型：
【题目】已知：
是最小的正整数，且
、满足
，请回答问题：
（1）请直接写出、、
的值：
________
________
________；
（2）、、所对应的点分别为
、
、
，点
是数轴上的一个动点，其对应的数为
，当点在0到2之间（即
）运动时，请化简
（请写出化简过程）；
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】2019 年 4 月 27 日，第二届“一带一路”国际合作高峰论坛圆满闭幕．“一带一路”已成为我国参与全球开放合作、改善全球经济治理体系、促进全球共同发展繁荣、推动构建人类命运共同体的中国方案．其中中欧班列见证了“一带一路”互联互通的跨越式发展，年运送货物总值由 2011 年的不足 6 亿美元，发展到 2018 年的约 160 亿美元．下面是 2011-2018 年中欧班列开行数量及年增长率的统计图．
根据图中提供的信息填空：
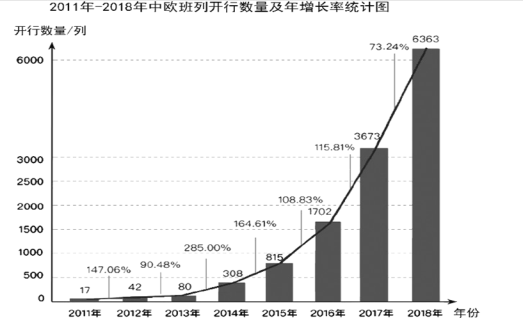
（1）2018 年，中欧班列开行数量的增长率是_____；
（2）如果 2019 年中欧班列的开行数量增长率不低于 50%，那么 2019 年中欧班列开行数量至少是_____列．
查看答案和解析>>
科目：初中数学 来源： 题型：
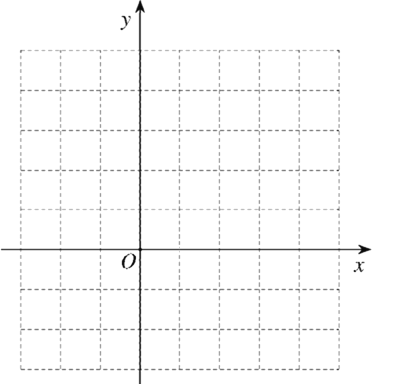
【题目】对于任意一点 P 和线段 a．若过点 P 向线段 a 所在直线作垂线，若垂足落在线段 a 上，则称点 P 为线段a 的内垂点．在平面直角坐标系 xOy 中，已知点 A(-1，0)，B(2，0 ) ，C(0，2)．
（1）在点 M（1，0），N（3，2），P（-1，-3）中，是线段 AB 的内垂点的是 ；
（2）已知点 D（-3，2），E（-3，4）．在图中画出区域并用阴影表示，使区域内的每个点均为 Rt△CDE三边的内垂点；
（3）已知直线 m 与 x 轴交于点 B，与 y 轴交于点 C，将直线 m 沿 y 轴平移 3 个单位长度得到直线 n ． 若存在点 Q，使线段 BQ 的内垂点形成的区域恰好是直线 m 和 n 之间的区域（包括边界），直接写出点 Q 的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在如图所示的网格中有四条线段AB、CD、EF、GH（线段端点在格点上），
⑴选取其中三条线段，使得这三条线段能围成一个直角三角形．
答：选取的三条线段为 ．
⑵只变动其中两条线段的位置，在原图中画出一个满足上题的直角三角形（顶点仍在格点，并标上必要的字母）．
答：画出的直角三角形为△ ．
⑶所画直角三角形的面积为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
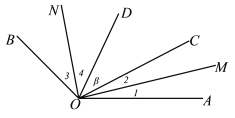
【题目】如图，射线OC、OD在∠AOB内部，∠AOB＝
，∠COD＝
，分别作∠AOC和∠BOD的平分线OM、ON，
（1）当＝130°，＝40°时，请你填空：∠1＋∠3＝______°，∠MON＝______°；
（2）聪明的小芳通过探究发现，当射线OC、OD的位置在∠AOB内变化时，∠MON与、之间总满足∠MON＝
，你是否认同她的这一结论？请说明理由；
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】观察下列各式：
···①，
···②，
…③，…
探索以上式子的规律．
（1）第7个式子是_______；
（2）试写出第
个等式，并说明第个等式成立；
（3）根据以上规律写出第2019个式子：______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知BD为∠ABC的平分线，DE⊥BC于E，且AB+BC=2BE.
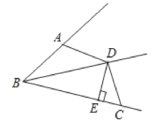
(1)求证：∠BAD+∠BCD=180°；
(2)若将条件“AB+BC=2BE”与结论“∠BAD+∠BCD=180°”互换，结论还成立吗?请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
