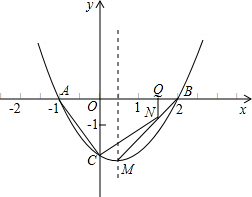
ŅŃÖŖ¶ž“ĪŗÆŹżµÄĶ¼ĻóČēĶ¼ĖłŹ¾£®
£Ø1£©Ē󶞓ĪŗÆŹżµÄ½āĪöŹ½¼°Å×ĪļĻ߶„µćMµÄ×ų±ź£»
£Ø2£©ČōµćNĪŖĻ߶ĪBMÉĻµÄŅ»µć£¬¹żµćN×÷xÖįµÄ“¹Ļߣ¬“¹×ćĪŖµćQ£®µ±µćNŌŚĻ߶ĪBMÉĻŌĖ¶ÆŹ±£ØµćN²»ÓėµćB£¬µćMÖŲŗĻ£©£¬ÉčNQµÄ³¤ĪŖt£¬ĖıߊĪNQACµÄĆ껿ĪŖs£¬ĒósÓėtÖ®¼äµÄŗÆŹż¹ŲĻµŹ½¼°×Ō±äĮætµÄȔֵ·¶Ī§£»
£Ø3£©ŌŚ¶Ō³ĘÖįÓŅ²ąµÄÅ×ĪļĻßÉĻŹĒ·ń“ęŌŚµćP£¬Ź¹”÷PACĪŖÖ±½ĒČż½ĒŠĪ£æČō“ęŌŚ£¬Ēó³öĖłÓŠ·ūŗĻĢõ¼žµÄµćPµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£»
£Ø4£©½«”÷OAC²¹³É¾ŲŠĪ£¬Ź¹ÉĻ”÷OACµÄĮ½øö¶„µć³ÉĪŖ¾ŲŠĪŅ»±ßµÄĮ½øö¶„µć£¬µŚČżøö¶„µćĀäŌŚ¾ŲŠĪÕāŅ»±ßµÄ¶Ō±ßÉĻ£¬ŹŌÖ±½ÓŠ“³ö¾ŲŠĪµÄĪ“ÖŖµÄ¶„µć×ų±ź£Ø²»ŠčŅŖ¼ĘĖć¹ż³Ģ£©£®

 ŅŃÖŖ¶ž“ĪŗÆŹżµÄĶ¼ĻóČēĶ¼ĖłŹ¾£®
ŅŃÖŖ¶ž“ĪŗÆŹżµÄĶ¼ĻóČēĶ¼ĖłŹ¾£® ½ā£ŗ£Ø1£©ÉčÅ×ĪļĻߵĽāĪöŹ½y=a£Øx+1£©£Øx-2£©£¬
½ā£ŗ£Ø1£©ÉčÅ×ĪļĻߵĽāĪöŹ½y=a£Øx+1£©£Øx-2£©£¬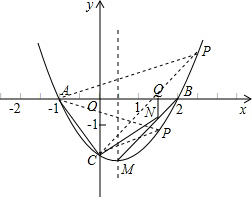
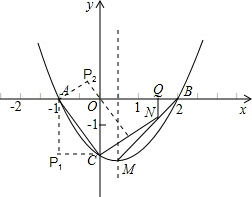



 14”¢ŅŃÖŖ¶ž“ĪŗÆŹżµÄĶ¼ĻóČēĶ¼ĖłŹ¾£¬ÄĒĆ““ĖŗÆŹżµÄ½āĪöŹ½æÉÄÜŹĒ£Ø””””£©
14”¢ŅŃÖŖ¶ž“ĪŗÆŹżµÄĶ¼ĻóČēĶ¼ĖłŹ¾£¬ÄĒĆ““ĖŗÆŹżµÄ½āĪöŹ½æÉÄÜŹĒ£Ø””””£©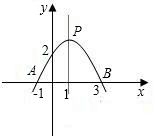 ŅŃÖŖ¶ž“ĪŗÆŹżµÄĶ¼ĻóČēĶ¼ĖłŹ¾£¬øł¾ŻĶ¼ÖŠµÄŹż¾Ż£¬
ŅŃÖŖ¶ž“ĪŗÆŹżµÄĶ¼ĻóČēĶ¼ĖłŹ¾£¬øł¾ŻĶ¼ÖŠµÄŹż¾Ż£¬ ŅŃÖŖ¶ž“ĪŗÆŹżµÄĶ¼ĻóČēÓŅĶ¼£¬ŌņĻĀĮŠ½įĀŪÖŠ£¬ÕżČ·µÄ½įĀŪÓŠ£Ø””””£©
ŅŃÖŖ¶ž“ĪŗÆŹżµÄĶ¼ĻóČēÓŅĶ¼£¬ŌņĻĀĮŠ½įĀŪÖŠ£¬ÕżČ·µÄ½įĀŪÓŠ£Ø””””£© ŅŃÖŖ¶ž“ĪŗÆŹżµÄĶ¼ĻóČēĶ¼ĖłŹ¾£¬
ŅŃÖŖ¶ž“ĪŗÆŹżµÄĶ¼ĻóČēĶ¼ĖłŹ¾£¬