
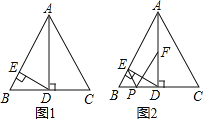
【题目】如图1,△ABC是边长为8的等边三角形,AD⊥BC下点D,DE⊥AB于点E
(1)求证:AE=3EB;
(2)若点F是AD的中点,点P是BC边上的动点,连接PE,PF,如图2所示,求PE+PF的最小值及此时BP的长;
(3)在(2)的条件下,连接EF,若AD=![]() ,当PE+PF取最小值时,△PEF的面积是 .
,当PE+PF取最小值时,△PEF的面积是 .
【答案】(1)见解析;(2)PE+PF的最小值=6,BP=2;(3)2![]()
【解析】
(1)解直角三角形求出BE,AE即可判断.
(2)如图2中,延长DF到H,使得DH=DF,连接EF,连接EH交BC于点P,此时PE+PF的值最小.证明∠HEF=90°,解直角三角形求出EH即可解决问题.
(3)证明△PBE是等边三角形,求出PE,EF即可解决问题.
(1)证明:如图1中,
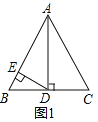
∵△ABC是等边三角形,
∴AB=BC=AC=8,∠B=∠BAC=60°
∵AD⊥BC,
∴BD=DC=4,
∵DE⊥AB,
∴∠DEB=90°,∠BDE=30°,
∴BE=![]() BD=2,
BD=2,
∴AE=AB﹣BE=8﹣2=6,
∴AE=3BE.
(2)解:如图2中,延长DF到H,使得DH=DF,连接EF,连接EH交BC于点P,此时PE+PF的值最小.
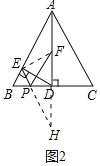
∵∠AED=90°,AF=FD,
∴EF=AF=DF,
∵DF=DH,
∴DE=DF=DH,
∴∠FEH=90°,
∵在Rt△ABD中,∠ADB=90°,BD=4,∠B=60°,
∴AD=BDtan60°=4![]() ,
,
∵∠BAD=![]() ∠BAC=30°,FE=FA,
∠BAC=30°,FE=FA,
∴∠FEA=∠FAE=30°,
∴∠EFH=60°,∠H=30°,
∵FH=AD=4![]() ,
,
∴EH=FHcos30°=6,
∴PE+PF的最小值=PE+PH=EH=6,
∵PD=DHsin30°=2,
∴BP=BD﹣PD=2.
(3)解:如图2中,∵BE=BP=2,∠B=60°,
∴△BPE是等边三角形,
∴PE=2,
∵∠PEF=90°,EF=AF=DF=2![]() ,
,
∴S△PEF=![]() PEEF=
PEEF=![]() ×2×2
×2×2![]() =2
=2![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
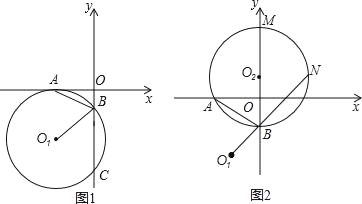
【题目】如图1在平面直角坐标系中,⊙O1与x轴切于A(﹣3,0)与y轴交于B、C两点,BC=8,连AB.
(1)求证:∠ABO1=∠ABO;
(2)求AB的长;
(3)如图2,过A、B两点作⊙O2与y轴的正半轴交于M,与O1B的延长线交于N,当⊙O2的大小变化时,得出下列两个结论:①BM﹣BN的值不变;②BM+BN的值不变.其中有且只有一个结论正确,请判断正确结论并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形![]() ,
,![]() ,
,![]() 与
与![]() 互补,以点
互补,以点![]() 为顶点作一个角,角的两边分别交线段
为顶点作一个角,角的两边分别交线段![]() ,
,![]() 于点
于点![]() ,
,![]() ,且
,且![]() ,连接
,连接![]() ,试探究:线段
,试探究:线段![]() ,
,![]() ,
,![]() 之间的数量关系.
之间的数量关系.
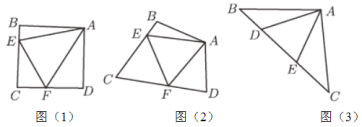
(1)如图(1),当![]() 时,
时,![]() ,
,![]() ,
,![]() 之间的数量关系为___________.
之间的数量关系为___________.
(2)在图(2)的条件下(即不存在![]() ),线段
),线段![]() ,
,![]() ,
,![]() 之间的数量关系是否仍然成立?若成立,请完成证明;若不成立,请说明理由.
之间的数量关系是否仍然成立?若成立,请完成证明;若不成立,请说明理由.
(3)如图(3),在腰长为![]() 的等腰直角三角形
的等腰直角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() 均在边
均在边![]() 上,且
上,且![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山地自行车越来越受中学生的喜爱.一网店经营的一个型号山地自行车,今年一月份销售额为30000元,二月份每辆车售价比一月份每辆车售价降价100元,若销售的数量与上一月销售的数量相同,则销售额是27000元.
(1)求二月份每辆车售价是多少元?
(2)为了促销,三月份每辆车售价比二月份每辆车售价降低了10%销售,网店仍可获利35%,求每辆山地自行车的进价是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为![]() ,连接AC、BD交于点O,CE平分∠ACD交BD于点E,
,连接AC、BD交于点O,CE平分∠ACD交BD于点E,
(1)求DE的长;
(2)过点EF作EF⊥CE,交AB于点F,求BF的长;
(3)过点E作EG⊥CE,交CD于点G,求DG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并解答问题.
面积与代数恒等式
通过学习,我们知道可以用图1的面积来解释公式![]() ,人们经常称作用面积解释代数恒等式实际上还有一些代数恒等式也可以用这种形式表示,如可用图2表示
,人们经常称作用面积解释代数恒等式实际上还有一些代数恒等式也可以用这种形式表示,如可用图2表示![]() .
.
请根据阅读材料,解答下列问题:
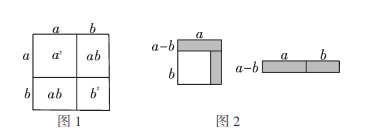
(1)请写出图3所表示的代数恒等式: ;
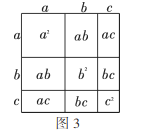
(2)试画一个几何图形,使它的面积表示:![]() ;
;
(3)请仿照上述方法另写一个含有![]() ,
,![]() 的代数恒等式,并画出与它对应的几何图形.
的代数恒等式,并画出与它对应的几何图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y1=a1x2+b1x+c1,y2=a2x2+b2x+c2且满足![]() (k≠0,1).则称抛物线y1,y2互为“友好抛物线”,则下列关于 “友好抛物线”的说法不正确的是( )
(k≠0,1).则称抛物线y1,y2互为“友好抛物线”,则下列关于 “友好抛物线”的说法不正确的是( )
A. y1,y2开口方向、开口大小不一定相同
B. 因为y1,y2的对称轴相同
C. 如果y2的最值为m,则y1的最值为km
D. 如果y2与x轴的两交点间距离为d,则y1与x轴的两交点间距离为|k|d
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点C是⊙O中直径AB上的一个动点,过点C作CD⊥AB交⊙O于点D,点M是直径AB上一固定点,作射线DM交⊙O于点N.已知AB=6cm,AM=2cm,设线段AC的长度为xcm,线段MN的长度为ycm.
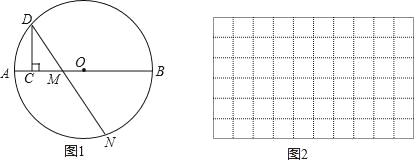
小东根据学习函数的经验,对函数y随自变量的变化而变化的规律进行了探索.
下面是小东的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了与y的几组值,如下表:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 4 | 3.3 | 2.8 | 2.5 |
| 2.1 | 2 |
(说明:补全表格时相关数值保留一位小数)
(2)在图2中建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:当AC=MN时,x的取值约为 cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com