
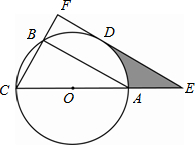
 (2012•高淳县一模)已知△ABC内接于⊙O,AC是⊙O的直径,D是
(2012•高淳县一模)已知△ABC内接于⊙O,AC是⊙O的直径,D是 | AB |
 |
| AB |
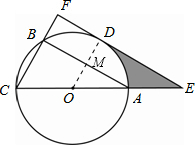 解:(1)直线EF与圆O相切,理由为:
解:(1)直线EF与圆O相切,理由为: |
| AB |
 |
| BD |
 |
| AD |
| CE2-CF2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| OD |
| FC |
| DE |
| EF |
| 4 |
| 6 |
| DE | ||
6
|
| 3 |
| 1 |
| 2 |
| 3 |
| 60•π•42 |
| 360 |
| 3 |
| 8π |
| 3 |


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案科目:初中数学 来源: 题型:

| 平均数(分) | 中位数(分) | 众数(分) | |
| (1)班 | 90 | 90 | |
| (2)班 | 88 | 100 |
查看答案和解析>>
科目:初中数学 来源: 题型:
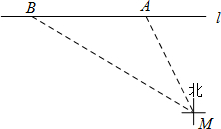 (2012•高淳县一模)《中华人民共和国道路交通管理条理》规定:“小汽车在城市街道公路上的行驶速度不得超过70km/h(即19.44m/s)”.如图所示,已知测速站M到街道公路l的距离为90m,一辆小汽车在街道公路l上由东向西行驶,测得此车从点A行驶到点B所用的时间为6s,并测得A在M的北偏西27°方向上,B在M的北偏西60°方向上.求出此车从A到B的平均速度,并判断此车是否超过限速.
(2012•高淳县一模)《中华人民共和国道路交通管理条理》规定:“小汽车在城市街道公路上的行驶速度不得超过70km/h(即19.44m/s)”.如图所示,已知测速站M到街道公路l的距离为90m,一辆小汽车在街道公路l上由东向西行驶,测得此车从点A行驶到点B所用的时间为6s,并测得A在M的北偏西27°方向上,B在M的北偏西60°方向上.求出此车从A到B的平均速度,并判断此车是否超过限速.| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 延长线交于点M,边B1A1与OB交于点N,边B1A1与OA的延长线交于点E,连接MN.
延长线交于点M,边B1A1与OB交于点N,边B1A1与OA的延长线交于点E,连接MN.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com