
【题目】已知在平面直角坐标系中,A(9,0),直线l:y=![]() .P,Q两点分别同时从O,A出发,P点沿直线l向上运动,Q点沿x轴向左运动,它们的速度相同.连接PQ,当
.P,Q两点分别同时从O,A出发,P点沿直线l向上运动,Q点沿x轴向左运动,它们的速度相同.连接PQ,当
PQ⊥x轴时,P,Q两点同时停止运动.设P点的横坐标为m(m≥0),
(1)求m的取值范围;
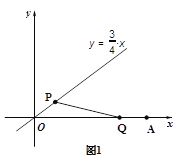
(2)如图1,当△OPQ是以OP为腰的等腰三角形时,求m的值;
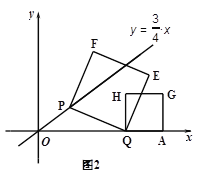
(3)如果以PQ为边在上方作正方形PQEF,以AQ为边在上方作正方形 QAGH,如图2,
①用含m的代数式表示E点的坐标;
②当正方形PQEF的某个顶点(Q点除外)落在正方形 QAGH的边上,请直接写出m的值.
【答案】(1)0≤m≤4;(2)![]() 或
或![]() .(3)①E(9-
.(3)①E(9-![]() m,9-
m,9-![]() );②m=4,
);②m=4, ![]() ,
,![]() .
.
【解析】
(1)直接将m点带入一次函数即可.
(2)讨论两个腰相等.
(3)过PE引x轴垂线,再讨论.
把x=m带入y= ![]() x得y=
x得y=![]() m,
m,
∴P(m,![]() m),∴OP=
m),∴OP=![]() =
=![]() ,
,
∵OP=AQ,∴AQ=![]() ,
,
∴OQ=9-![]() , ∵PQ⊥x轴时,运动停止,
, ∵PQ⊥x轴时,运动停止,
∴OH≤OQ, ∴m≤9-![]() ,且m≥0.
,且m≥0.
∴0≤m≤4.
(2)若OP=PQ,则OH=![]() OQ,∴m=
OQ,∴m=![]() (9-
(9-![]() ),m=
),m=![]() ,
,
若OP=OQ则![]() =9-
=9-![]() ,m=
,m=![]() .
.
∴m=![]() 或
或![]() .
.
(3) 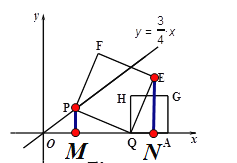
①易证PMQ≌QNE,∴QN=PM=![]() m,
m,
∴ON=OQ+QN
=9-![]() +
+![]() m
m
=9-![]() m
m
且EN=MQ=OQ-OM=9-![]() -m=9-
-m=9-![]()
∴E(9-![]() m,9-
m,9-![]() )
)
②易求F(![]() ,
,![]() ),
),
若点P在HQ上,则m=9-![]() ,m=4.
,m=4.
若点F在HG上,则![]() =
=![]() ,m=
,m=![]() .
.
若点F在AG上,则![]() =9,m=
=9,m=![]() .(舍)
.(舍)
若点E在HG上,则9-![]() =
=![]() ,m=
,m=![]() .
.
若点E在HG上,则9-![]() m=9,m=0(舍).
m=9,m=0(舍).
∴m=4, ![]() ,
,![]() .
.


科目:初中数学 来源: 题型:
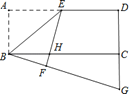
【题目】已知如图,在长方形ABCD中,点E是AD的中点,连结BE,将△ABE沿着BE翻折得到△FBE,EF交BC于点H,延长BF、DC相交于点G,若DG=16,BC=24,则AB=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AD=BC,AB=CD,AD>AB,将长方形ABCD折叠,使点C与点A重合,折痕为MN,连接CN.若△CDN的面积与△CMN的面积比为1:3,
(1)求证:DN=BM;(2)求ND:NA的值;(3)求MN2:BM2的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y= ![]() x﹣3与x轴、y轴分别交于A、B两点,P在以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB,则△PAB面积的最大值是 .
x﹣3与x轴、y轴分别交于A、B两点,P在以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB,则△PAB面积的最大值是 . 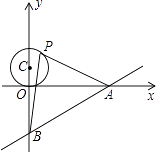
查看答案和解析>>
科目:初中数学 来源: 题型:
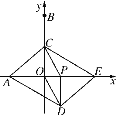
【题目】如图,在平面直角坐标系中,点A,B的坐标分别是(-3,0),(0,6),动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C从点B出发,沿射线BO方向以每秒2个单位的速度运动.以CP,CO为邻边构造PCOD.在线段OP延长线上一动点E,且满足PE=AO.
(1)当点C在线段OB上运动时,求证:四边形ADEC为平行四边形;
(2)当点P运动的时间为![]() 秒时,求此时四边形ADEC的周长是多少.
秒时,求此时四边形ADEC的周长是多少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com