
����Ŀ����ͼ�٣�������y��ax2+bx+3��a��0����x�ᡢy��ֱ���A����1��0����B��3��0����C���㣮
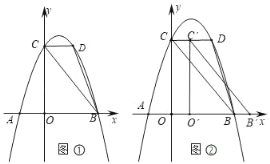
��1����a��b��ֵ��
��2����D��2��m���ڵ�һ�����������ϣ�����BC��BD��CD���ڶԳ��������������ϴ���һ��P�������PBC����DBC���������P�����ꣻ
��3����ͼ�ڣ��ڣ�2���������½���BOC��x����������ÿ��1����λ���ȵ��ٶ�����ƽ�ƣ���ƽ�ƺ��������Ϊ��B'O'C'��ƽ�ƹ����У���B'O'C'����BCD�ص����ֵ������ΪS����ƽ�Ƶ�ʱ��Ϊt�룬��ֱ��д��S��t֮��ĺ�����ϵʽ����ע���Ա�����ȡֵ��Χ����
���𰸡���1��a����1��b��2����2�����ڣ�P����![]() ��
��![]() ������3��
������3��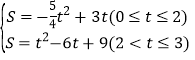 ��
��
��������
��1������A��B�������ʽ�������a��b��ֵ��
��2��������֪���������D�����꣬�������߶�OC��OB��ȡ�CD��x�ἰ��������������֤����CDB�ա�CGB������ȫ�������������G�����꣬���ֱ��BP�Ľ���ʽ���������κ�������ʽ�������P�����꣮
��3���������������һ������ص����Ϊ�ı��Σ����ô������μ�ȥ����С��������ý���ʽ���ڶ�������ص�����Ϊ�����Σ������������ε������ʽ��ã�
��1������A����1��0����B��3��0�����������ߣ�
![]() ��
��
���a����1��b��2��
��2�����ڣ�
����D���������ߵĽ���ʽ�ã�m��3��
��D��2��3����
��x��0��y��3��
��C��0��3����
��OC��OB��
���OCB����CBO��45����
��ͼ1��ʾ��
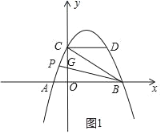
��CD��x�ᣬ
���DCB����BCO��45����
����CDB����CGB��
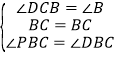
���CDB�ա�CGB��ASA����
��CG��GD��2��
��OG��1��
��G��0��1����
��ֱ��BP��y��kx+1��
�����B��
��k����![]() ��
��
��ֱ��BP��y����![]() x+1��
x+1��
����ֱ��BP�Ͷ��κ�������ʽ��
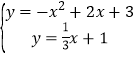
���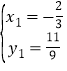 ��
��![]() ���ᣩ��
���ᣩ��
��P![]() ��
��
��3��ֱ��BC��y����x+3��ֱ��BD��y����3x+9��
��0��t��2ʱ����ͼ2��ʾ��
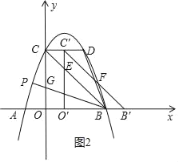
��ֱ��B��C����y������x��t��+3��
����ֱ��BD���F��![]() ����
����
S��![]() ��
��
��2��t��3ʱ����ͼ3��ʾ��
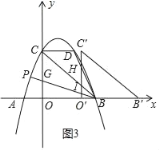
H��t����3t+9����I��t����t+3����
S��![]() ����3��t����t2��6t+9��
����3��t����t2��6t+9��
����������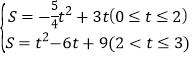 ��
��


 Сѧ��ʱ��ҵȫͨ����ϵ�д�
Сѧ��ʱ��ҵȫͨ����ϵ�д� �����ÿ�ʱѵ��ϵ�д�
�����ÿ�ʱѵ��ϵ�д� ��Ԫȫ��������ϵ�д�
��Ԫȫ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Ǵ��ϲ���ּ���һ�������˶�,��������ʱ,��Ҫ����ͬƵ˦������,������˦����ߴ�ʱ,����״�ɽ��ƿ���������,��ͼ��С����С��˦���ӵ���ߴ�ʱ��ʾ��ͼ,���������ӵ���֮��ľ���Ϊ4![]() ,�����ĸ߶�Ϊ1
,�����ĸ߶�Ϊ1![]() ,��С����������λ��Ϊԭ�㽨��ƽ��ֱ������ϵ.
,��С����������λ��Ϊԭ�㽨��ƽ��ֱ������ϵ.
(1)������Ϊ15![]() ��С��վ�����ӵ����·�,�Ҿ�С���������ֵ��Ҳ�1
��С��վ�����ӵ����·�,�Ҿ�С���������ֵ��Ҳ�1![]() ��ʱ,���Ӹպ�ͨ��С���ͷ��,����������Ӧ�������ߵı���ʽ;
��ʱ,���Ӹպ�ͨ��С���ͷ��,����������Ӧ�������ߵı���ʽ;
(2)������Ϊ![]() ��С��Ҳվ�����ӵ����·�.
��С��Ҳվ�����ӵ����·�.
�ٵ�С���ھ�С���������ֵ����1.5![]() ��ʱ,����������С����ͷ��?��˵�����ɣ�
��ʱ,����������С����ͷ��?��˵�����ɣ�
����С����С����������֮���ˮƽ����Ϊ![]() ,Ϊ��֤���Ӳ�����С����ͷ��,��
,Ϊ��֤���Ӳ�����С����ͷ��,��![]() ��ȡֵ��Χ.(�ο�����:
��ȡֵ��Χ.(�ο�����: ![]() ȡ3.16)
ȡ3.16)

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ![]() �У�����
�У�����![]() ��ͼ����
��ͼ����![]() ��ֱ��
��ֱ��![]() ��x�ύ�ڵ�
��x�ύ�ڵ�![]() ��
��
��1����![]() ��ֵ��
��ֵ��
��2�����ڶ����ĵ�![]() ��ƽ����x���ֱ�ߣ���ֱ��
��ƽ����x���ֱ�ߣ���ֱ��![]() �ڵ�C��������
�ڵ�C��������![]() ��ͼ���ڵ�D��
��ͼ���ڵ�D��
�ٵ�![]() ʱ���ж��߶�PD��PC��������ϵ����˵�����ɣ�
ʱ���ж��߶�PD��PC��������ϵ����˵�����ɣ�
����![]() ����Ϻ�����ͼ��ֱ��д��n��ȡֵ��Χ��
����Ϻ�����ͼ��ֱ��д��n��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���D�DZ�BC�ϵĵ㣨��B��C���㲻�غϣ�������D��DE��AC��DF��AB���ֱ�AB��AC��E��F���㣬����˵����ȷ���ǣ�������
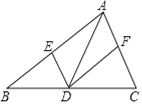
A. ��AD��BC�����ı���AEDF�Ǿ���
B. ��AD��ֱƽ��BC�����ı���AEDF�Ǿ���
C. ��BD=CD�����ı���AEDF������
D. ��ADƽ�֡�BAC�����ı���AEDF������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����BAD������BEC��ƽ�����Ƶ�B��ת60�����ã���AB��BC��BE��CE������DE.
��1����֤����BDE�ա�BCE��
��2�����ж��ı���ABED����״����˵�����ɣ�
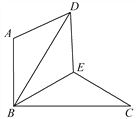
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��![]() �У�
��![]() ����
����![]() ��
��![]() �ϣ�
�ϣ�![]() ����
����![]() Ϊֱ����
Ϊֱ����![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() ���ҵ�
���ҵ�![]() Ϊ�е㣬����
Ϊ�е㣬����![]() ��
��![]() .
.
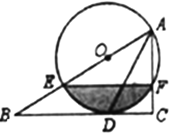
��1����֤��![]() ƽ��
ƽ��![]() ��
��
��2������Ӱ�������.���������![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
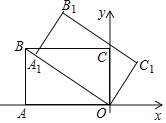
����Ŀ����ͼ��ƽ��ֱ������ϵ�У�����OABC�Ķ���A����6��0����C��0��2![]() ����������OABC�Ƶ�O˳ʱ�뷽����ת��ʹ��Aǡ������OB�ϵĵ�A1�������B�Ķ�Ӧ��B1������Ϊ_____��
����������OABC�Ƶ�O˳ʱ�뷽����ת��ʹ��Aǡ������OB�ϵĵ�A1�������B�Ķ�Ӧ��B1������Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
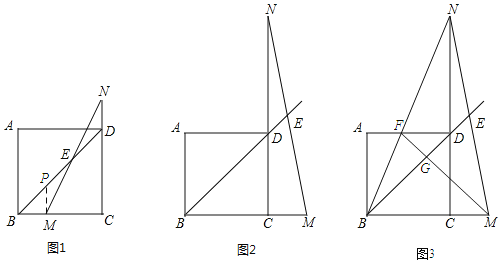
����Ŀ����������ABCD�У���M������BC��һ�㣬��N��CD�ӳ�����һ�㣬��BM��DN��ֱ��BD��MN���ڵ�E��
��1����ͼ1������M��BC��ʱ��Ϊ֤����BD��2DE��![]() BM����һ���ۣ�С�������˸����ߣ�����M��CD��ƽ���߽�BD�ڵ�P���������һ˼·������С����ɽ���ȥ��֤�����̣�
BM����һ���ۣ�С�������˸����ߣ�����M��CD��ƽ���߽�BD�ڵ�P���������һ˼·������С����ɽ���ȥ��֤�����̣�
��2����ͼ2������M��BC���ӳ�����ʱ����BD��DE��BM֮�������������ϵ���� ����
��3���ڣ�2���������£�����BN��AD�ڵ�F������MF��BD�ڵ�G����ͼ3����![]() CM��2�����߶�DG���� ����
CM��2�����߶�DG���� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ������չ��������������������������������������ܲ������˶���Ŀ��Ϊ�˽�ѧ����ϲ����һ����Ŀ�������ȡ�˲���ѧ�����е��飬�����������µ�����ͳ��ͼ������ͳ��ͼ��������Ϣδ��������
��1���α������ѧ��������
��2����ȫ����ͳ��ͼ��
��3����У����3000��ѧ���������ȫУ��ϲ���������������ϲ���������������٣�

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com