
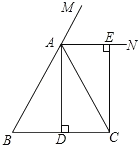
【题目】已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
【答案】(1)证明见解析(2)当△ABC满足∠BAC=90°时,四边形ADCE是一个正方形.
【解析】试题分析:(1)根据矩形的有三个角是直角的四边形是矩形,已知CE⊥AN,AD⊥BC,所以求证∠DAE=90°,可以证明四边形ADCE为矩形.
(2)根据正方形的判定,我们可以假设当AD=![]() BC,由已知可得,DC=
BC,由已知可得,DC=![]() BC,由(1)的结论可知四边形ADCE为矩形,所以证得,四边形ADCE为正方形.
BC,由(1)的结论可知四边形ADCE为矩形,所以证得,四边形ADCE为正方形.
试题解析:(1)证明:在△ABC中,AB=AC,AD⊥BC,
∴∠BAD=∠DAC,
∵AN是△ABC外角∠CAM的平分线,
∴∠MAE=∠CAE,
∴∠DAE=∠DAC+∠CAE=![]() ×180°=90°,
×180°=90°,
又∵AD⊥BC,CE⊥AN,
∴∠ADC=∠CEA=90°,
∴四边形ADCE为矩形.
(2)当△ABC满足∠BAC=90°时,四边形ADCE是一个正方形.
理由:∵AB=AC,
∴∠ACB=∠B=45°,
∵AD⊥BC,
∴∠CAD=∠ACD=45°,
∴DC=AD,
∵四边形ADCE为矩形,
∴矩形ADCE是正方形.
∴当∠BAC=90°时,四边形ADCE是一个正方形.


科目:初中数学 来源: 题型:
【题目】列方程组解应用题:某学校在筹建数学实验室过程中,准备购进一批桌椅,现有三种桌椅可供选择:甲种每套150元,乙种每套210元,丙种每套250元。若该学校同时购买其中两种不同型号的桌椅50套,恰好花费了9000元,则共有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转动甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则李燕获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).
(1)请用列表或画树状图的方法表示出上述游戏中两数和的所有可能的结果;
(2)分别求出李燕和刘凯获胜的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
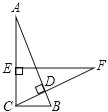
【题目】如图,Rt△ABC中,∠ACB=90°, BC=3cm, CD⊥AB于D, 在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,若EF=5cm,求AE.
查看答案和解析>>
科目:初中数学 来源: 题型:
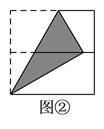
【题目】如图,将正方形对折后展开(图④是连续两次对折后再展开),再按图示方法折叠,能够得到一个直角三角形(阴影部分),且它的一条直角边等于斜边的一半,这样的图形有( ).



A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,∠AOB=∠COD=90°,射线OE,FO分别平分∠AOC和∠BOD.
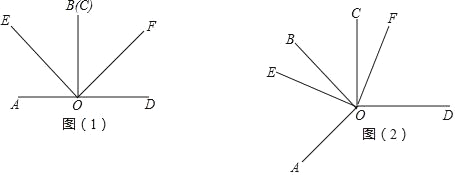
(1)当OB和OC重合时,如图(1),求∠EOF的度数;
(2)当∠AOB绕点O逆时针旋转至图(2)的位置(0°<∠BOC<90°)时,求∠EOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上线段AB=2(单位长度),CD=4(单位长度),点A在数轴上表示的数是﹣4,点C在数轴上表示的数是4,若线段AB以3个单位长度/秒的速度向右匀速运动,同时线段CD以1个单位长度/秒的速度向左匀速运动.
![]()
(1)问运动多少秒时BC=2(单位长度)?
(2)线段AB与线段CD从开始相遇到完全离开共经过多长时间?
(3)P是线段AB上一点,当B点运动到线段CD上,且点P不在线段CD上时,是否存在关系式BD﹣AP=3PC.若存在,求线段PD的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李大爷按每千克2.1元批发了一批黄瓜到镇上出售,为了方便,他带了一些零钱备用.他先按市场售出一些后,又降低出售.售出黄瓜千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示,结合图象回答下列问题:
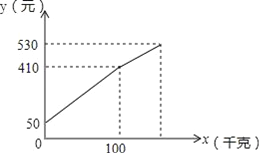
(1)李大爷自带的零钱是多少?
(2)降价前他每千克黄瓜出售的价格是多少?
(3)卖了几天,黄瓜卖相不好了,随后他按每千克下降1.6元将剩余的黄瓜售完,这时他手中的钱(含备用的钱)是530元,问他一共批发了多少千克的黄瓜?
(4)请问李大爷亏了还是赚了?若亏(赚)了,亏(赚)多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:求l+2+22+23+24+…+22013的值.
解:设S=l+2+22+23+24+…+22012+22013,将等式两边同时乘2,
得2S=2+22+23+24+25+…+22013+22014. 将下式减去上式,得2S﹣S=22014-1
即S=22014-1,
即1+2+22+23+24+…+22013=22014-1
仿照此法计算:(1)1+3+32+33+…+3100;(2)1+![]() +
+![]() +
+![]() +…+
+…+![]() ,
,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com