
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��A����5��0����B��5��0����D��2��7��������AD����y���ڵ�C��
��1����C�������� ����
��2������P��B�������ÿ��1����λ���ٶ���BA�����˶���ͬʱ����Q��C�������Ҳ��ÿ��1����λ���ٶ���y�������᷽���˶�����P���˶���A��ʱ�����㶼ֹͣ�˶�������ӳ������˶���x�룮
�����ú�x�Ĵ���ʽ�ֱ��ʾP��Q��������ꣻ
����x��2ʱ��y�����Ƿ����һ��E��ʹ�á�AQE��������APQ�������ȣ������ڣ���E�����꣬�������ڣ�˵�����ɣ�
��3���ڣ�2���������£��ڵ�P��Q�˶������У�����Q��x���ƽ����OF����G��F�ֱ�λ��y����������ࣩ����GQP���APQ�Ľ�ƽ���߽��ڵ�M�����PMQ�Ĵ�С�����P��Q���˶����仯��������仯���������PMQ�Ķ������������仯����˵�����ɣ�

���𰸡���1����0��5������2����P��5��x��0����Q��0��5+x���������ڣ���E������Ϊ��0��18.2����0����4.2������3����PMQ�Ķ������䣬ֵΪ90�㣮
��������
��1����DE��x�ᣬ���ݵ���������AE��DE��AO�����ݵ���ֱ�������ε����ʽ�ɣ�
��2���ٸ������⡢���ͼ�ν��
�ڷ�E��y����������E��y��ĸ�����������������������ε������ʽ���㼴�ɣ�
��3���ó���GQP+��APQ��180���������PQM+��QPM��90�������PMQ�Ķ������䣮
��1����DE��x�ᣬ
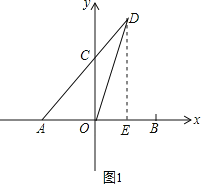
��A����5��0����D��2��7����
��AE��DE��7��AO��5��
�ߡ�CAO����DAEΪֱ�������Σ�
���CAO��45����
���CAO�ǵ���ֱ�������Σ�
��CO��AO��5��
��C��0��5����
�ʴ�Ϊ����0��5����
��2���١߶���P��B�������ÿ��1����λ���ٶ���BA�����˶���B��5��0����
��P��5��x��0����
�߶���Q��C�������ÿ��1����λ���ٶ���y�������᷽���˶���C��0��5����
��Q��0��5+x����
��P��5��x��0����Q��0��5+x����
�ڴ��ڣ���E������Ϊ��0��y����
��x��2ʱ��S��APQ����5+3����7��2��28��
���һ��E��y��������ᣮ
��y��7����5��2��28��
��y��18.2��
��E��0��18.2����
�������E��y��ĸ����ᣬ
��7��y����5��2��28��
��y����4.2��
��E��0����4.2����
���E����������0��18.2����0����4.2����
��3�����䣮

��GF��x�ᣬ
���GQP+��APQ��180����
��QM��PM�ֱ�ƽ�֡�GQP����APQ��
���PQM��![]() ��GQP����QPM��
��GQP����QPM��![]() ��APQ��
��APQ��
���PQM+��QPM��![]() ��GQP+
��GQP+![]() ��APQ��
��APQ��![]() ����GQP+��APQ����
����GQP+��APQ����![]() ��180����90����
��180����90����
�ߡ�PMQ+��PQM+��QPM��180����
���PMQ��180��������PQM+��QPM����180����90����90����
���PMQ�Ķ������䣮


 ����ѧ���ʱѧ����ϵ�д�
����ѧ���ʱѧ����ϵ�д� �ʰ�Ӣ��ͬ����ϰ��ϵ�д�
�ʰ�Ӣ��ͬ����ϰ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����PΪ������y=![]() x2��һ���㣮
x2��һ���㣮
��1����������y=![]() x2����������y=
x2����������y=![]() ��x+2��2��1ͨ��ͼ��ƽ�Ƶõ��ģ���д��ƽ�ƵĹ��̣�
��x+2��2��1ͨ��ͼ��ƽ�Ƶõ��ģ���д��ƽ�ƵĹ��̣�
��2����ֱ��l����y����һ��N����ƽ����x�ᣬ��N������Ϊ��0����1��������P��PM��l��M��
������̽������ͼһ���ڶԳ������Ƿ����һ����F��ʹ��PM=PF������������ڣ������F�����꣺�������ڣ���˵�����ɣ�
������������ͼ��������Q������Ϊ��1.5������QP+PF����Сֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Բ O �İ뾶Ϊ 1������ A(2��0)��ֱ����Բ O �����ڵ� B���� y ���ཻ�ڵ� C��
(1)�� AB �ij���
(2)��ֱ�� AB �Ľ���ʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ϵ![]() �У�
��![]() ��
��![]() ��
��![]() ���߶�
���߶�![]() �Ͽ�����
�Ͽ�����![]() �����ȷֵ�.
�����ȷֵ�.

��1������![]() ��
��![]() ���ϵ�һ���㣬����
���ϵ�һ���㣬����![]() ��
��![]() ����
����![]() ��ֵ��Сʱ�������
��ֵ��Сʱ�������![]() �����꼰
�����꼰![]() ����Сֵ��
����Сֵ��
��2����ͼ2������![]() ��
��![]() ����
����![]() �ڵ�
�ڵ�![]() ���ٽ�
���ٽ�![]() �Ƶ�
�Ƶ�![]() ��˳ʱ�뷽����ת����ת�Ƕ�Ϊ
��˳ʱ�뷽����ת����ת�Ƕ�Ϊ![]() ������ת�е�������Ϊ
������ת�е�������Ϊ![]() ������ת�����У�ֱ��
������ת�����У�ֱ��![]() ��ֱ��
��ֱ��![]() �Ľ���Ϊ
�Ľ���Ϊ![]() ��ֱ��
��ֱ��![]() ��ֱ��
��ֱ��![]() ���ڵ�
���ڵ�![]() ����
����![]() Ϊ����������ʱ����ֱ��д��
Ϊ����������ʱ����ֱ��д��![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ݮ�����϶��ʢ����һ��ˮ��������ijˮ�����۵��ڲ�ݮ���������������۳ɱ�Ϊÿǧ��20Ԫ�IJ�ݮ���涨�����ڼ����۵��۲����ڳɱ����ۣ�Ҳ������ÿǧ��40Ԫ�����������֣�������y(ǧ��)�����۵���x(Ԫ)����һ�κ�����ϵ����ͼ��y��x�ĺ�����ϵͼ��
(1)��y��x�ĺ�������ʽ��
(2)���ˮ�����۵�������ݮ��õ�����ΪWԪ����W�����ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
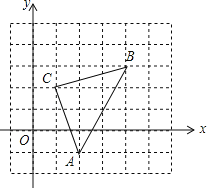
����Ŀ����ͼ��ֱ������ϵ�У���ABC�Ķ��㶼��������ϣ����У�C������Ϊ��1��2����
��1����գ���A���������� ������B���������� ����
��2������ABC������ƽ��2����λ���ȣ�������ƽ��1����λ���ȣ��õ���A��B��C�䣮��д����A��B��C��������������ꣻ
��3�����ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD���ܳ���20 cm����AB��ADΪ��������������ABEF��������ADGH����������ABEF��ADGH�����֮��Ϊ68 cm2����ô����ABCD�������_______cm2��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2+2x+m��2=0������ʵ������mΪ���������Ҹ÷��̵ĸ��������������������������������m�ĺ�Ϊ��������
A. 6 B. 5 C. 4 D. 3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��AEB��Rt��AFC�У�BE��AC�ཻ�ڵ�M����CF�ཻ�ڵ�D��AB��CF�ཻ��N����E����F��90�㣬��EAC����FAB��AE��AF.�������н��ۣ��١�B����C����CD��DN����BE��CF���ܡ�ACN�ա�ABM.������ȷ�Ľ�����(����)

A. �٢ۢ� B. �ڢۢ� C. �٢ڢ� D. �٢ڢ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com