
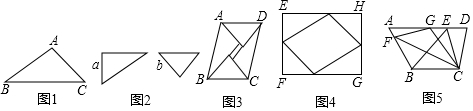
分析 回顾:如图1中,作AH⊥BC.求出AH即可解决问题;
探究:如图2中,根据S四边形ABCD=BC•AB•sin75°=2S△ABE+2S△BFC+S矩形EFGH列出方程即可解决问题;
应用:①作C关于AD的对称点H,CH交AD于J,连接BH,EH.因为EC=EH,推出EB+EC=EB+EH,在△EBH中,BE+EH≥BH,推出BE+EC的最小值为BH,求出BH即可解决问题;
②结论:点G不是AD的中点.理由反证法证明即可.
解答 由题意可知四边形EFGH是矩形,AB=CD=2a,AH=DH=BF=CF=b,EF=GH=$\sqrt{3}$a-b,EH=FG=b-a,BC=$\sqrt{2}$b,
解:回顾:如图1中,作AH⊥BC.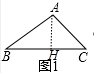
在Rt△ABH中,∵∠B=30°,AB=3,
∴AH=AB•sin30°=$\frac{3}{2}$,
∴S△ABC=$\frac{1}{2}$•BC•AH=$\frac{1}{2}$×4×$\frac{3}{2}$=3,
故答案为3.
探究:如图2中,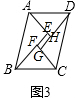
由题意可知四边形EFGH是矩形,AB=CD=2a,AH=DH=BF=CF=b,EF=GH=$\sqrt{3}$a-b,EH=FG=b-a,BC=$\sqrt{2}$b,
∵S四边形ABCD=BC•AB•sin75°=2S△ABE+2S△BFC+S矩形EFGH
∴$\sqrt{2}$b•2a•sin75°=2×$\frac{1}{2}$×a×$\sqrt{3}$a+2×$\frac{1}{2}$×b2+($\sqrt{3}$a-b)(b-a),
∴2$\sqrt{2}$absin75°=$\sqrt{3}$ab+ab,
∴sin75°=$\frac{\sqrt{6}+\sqrt{2}}{4}$.
如图3中,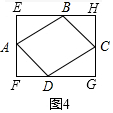
易知四边形ABCD是平行四边形,∠BAD=75°,
∴S四边形EFGH=2•S△ABE+2•S△ADF+S平行四边形ABCD,
∴(a+b)($\sqrt{3}$a+b)═2×$\frac{1}{2}$×a×$\sqrt{3}$a+2×$\frac{1}{2}$×b2+$\sqrt{2}$b•2a•sin75°,
∴sin75°=$\frac{\sqrt{6}+\sqrt{2}}{4}$.
应用:①作C关于AD的对称点H,CH交AD于J,连接BH,EH.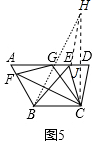
在Rt△DCJ中,JC=CD•sin75°=$\frac{5}{4}$($\sqrt{6}$+$\sqrt{2}$),
∴CH=2CJ=$\frac{5}{2}$($\sqrt{6}$+$\sqrt{2}$),
在Rt△BHC中,BH2=BC2+CH2=36+$\frac{25}{4}$($\sqrt{6}$+$\sqrt{2}$)2=86+25$\sqrt{3}$,
∵EC=EH,
∴EB+EC=EB+EH,
在△EBH中,BE+EH≥BH,
∴BE+EC的最小值为BH,
∴t=BE+CE,t2的最小值为BH2,即为86+25$\sqrt{3}$.
②结论:点G不是AD的中点.
理由:作CJ⊥AD于J,DH⊥CG于H.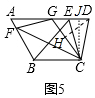
不妨设AG=GD=5,∵CD=5,
∴DC=DG,∵DH⊥CG,
∴GH=CH=3,
在Rt△CDH中,DH=$\sqrt{C{D}^{2}-C{H}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∵S△DGC=$\frac{1}{2}$•CG•DH=$\frac{1}{2}$•DG•CJ,
∴CJ=$\frac{24}{5}$,
∴sin∠CDJ=$\frac{CJ}{CD}$=$\frac{24}{25}$,
∵∠CDJ=75°,
∴与sin75°=$\frac{\sqrt{6}+\sqrt{2}}{4}$矛盾,
∴假设不成立,
∴点G不是AD的中点.
点评 本题考查四边形综合题、锐角三角函数、勾股定理、三角形的面积.轴对称最短问题等知识,解题的关键是学会理由分割法求四边形的面积,学会用反证法解决问题,属于中考压轴题.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:初中数学 来源: 题型:解答题
| 成本 (单位:万元/亩) | 销售额 (单位:万元/亩) | |
| 郁金香 | 2.4 | 3 |
| 玫瑰 | 2 | 2.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
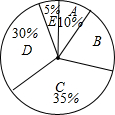 自来水公司调查了若干用户的月用水量x(单位:吨),按月用水量将用户分成A、B、C、D、E五组进行统计,并制作了如图所示的扇形统计图,已知除B组以外,参与调查的用户共64户,则所有参与调查的用户中用水量在6吨以下的共有( )
自来水公司调查了若干用户的月用水量x(单位:吨),按月用水量将用户分成A、B、C、D、E五组进行统计,并制作了如图所示的扇形统计图,已知除B组以外,参与调查的用户共64户,则所有参与调查的用户中用水量在6吨以下的共有( ) | 组别 | 月用水量x(单位:吨) |
| A | 0≤x<3 |
| B | 3≤x<6 |
| C | 6≤x<9 |
| D | 9≤x<12 |
| E | x>12 |
| A. | 18户 | B. | 20户 | C. | 22户 | D. | 24户 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 变为s2+300 | B. | 不变 | C. | 变大了 | D. | 变小了 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
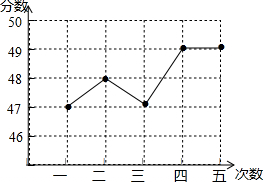 某中学九年级学生进行了五次体育模拟测试,甲同学的测试
某中学九年级学生进行了五次体育模拟测试,甲同学的测试| 次 数 | 一 | 二 | 三 | 四 | 五 |
| 分 数 | 46 | 47 | 48 | 49 | 50 |
| 中位数 | 平均数 | 方差 | |
| 甲 | 48 | 48 | 2 |
| 乙 | 48 | 48 | 0.8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com