
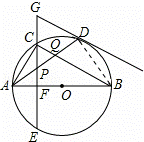
如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是![]() 的中点,弦CE⊥AB于点F,过点D的切线交EC的延长线于点G,连接AD,分别交CF、BC于点P、Q,连接AC.给出下列结论:
的中点,弦CE⊥AB于点F,过点D的切线交EC的延长线于点G,连接AD,分别交CF、BC于点P、Q,连接AC.给出下列结论:
①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心;④AP•AD=CQ•CB.
其中正确的是 (写出所有正确结论的序号).

考点:切线的性质;圆周角定理;三角形的外接圆与外心;相似三角形的判定与性质。
解答:解:∠BAD与∠ABC不一定相等,选项①错误;
连接BD,如图所示:
∵GD为圆O的切线,
∴∠GDP=∠ABD,
又AB为圆O的直径,∴∠ADB=90°,
∵CE⊥AB,∴∠AFP=90°,
∴∠ADB=∠AFP,又∠PAF=∠BAD,
∴△APF∽△ABD,
∴∠ABD=∠APF,又∠APF=∠GPD,
∴∠GDP=∠GPD,
∴GP=GD,选项②正确;
∵直径AB⊥CE,
∴A为![]() 的中点,即
的中点,即![]() =
=![]() ,
,
又C为![]() 的中点,∴
的中点,∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴∠CAP=∠ACP,
∴AP=CP,
又AB为圆O的直径,∴∠ACQ=90°,
∴∠PCQ=∠PQC,
∴PC=PQ,
∴AP=PQ,即P为Rt△ACQ斜边AQ的中点,
∴P为Rt△ACQ的外心,选项③正确;
连接CD,如图所示:

∵![]() =
=![]() ,
,
∴∠B=∠CAD,又∠ACQ=∠BCA,
∴△ACQ∽△BCA,
∴![]() =
=![]() ,即AC2=CQ•CB,
,即AC2=CQ•CB,
∵![]() =
=![]() ,
,
∴∠ACP=∠ADC,又∠CAP=∠DAC,
∴△ACP∽△ADC,
∴![]() =
=![]() ,即AC2=AP•AD,
,即AC2=AP•AD,
∴AP•AD=CQ•CB,选项④正确,
则正确的选项序号有②③④.
故答案为:②③④


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com