

分析 (1)先判定△ABE≌△CBD,再根据全等三角形对应边相等,对应角相等得出结论;
(2)先判定△ABE≌△CBD,再根据全等三角形对应边相等,对应角相等即可得出结论;
(3)先判定△AEB∽△CDB,再根据相似三角形对应边成比例,对应角相等进行推导,即可得出结论.
解答 解:(1)在△ABE和△CBD中,
$\left\{\begin{array}{l}{AB=CB}\\{∠ABE=∠CBD}\\{EB=DB}\end{array}\right.$,
∴△ABE≌△CBD(SAS),
∴AE=CD,且∠AEB=∠CDB,
∵∠CDB+∠BCD=90°,
∴∠AEB+∠BCD=90°,
∴∠CKE=90°,即AE⊥CD.
(2)AE=CD,AE⊥CD.
证明:∵∠DBE=∠ABC=90°,
∴∠DBE+∠ABD=∠ABC+∠ABD,
即∠ABE=∠CBD,
在△ABE和△CBD中,
$\left\{\begin{array}{l}{AB=CB}\\{∠ABE=∠CBD}\\{EB=DB}\end{array}\right.$,
∴△ABE≌△CBD(SAS),
∴AE=CD,且∠BAE=∠BCD,
∵∠BCD+∠BOC=90°,∠BOC=∠AOK,
∴∠AOK+∠BAE=90°,
∴∠AKO=90°,即AE⊥CD.
(3)AE=$\frac{1}{k}$CD,AE⊥CD.
证明:∵AB=kBC,DB=kEB,
∴$\frac{AB}{BC}=\frac{BE}{BD}=\frac{1}{k}$,
∵∠DBE=∠ABC=90°,
∴∠DBE+∠ABD=∠ABC+∠ABD,
即∠ABE=∠CBD,
∴△AEB∽△CDB,
∴$\frac{AE}{CD}=\frac{AB}{BC}=\frac{1}{k}$,且∠EAB=∠DCB,
∴AE=$\frac{1}{k}$CD,
∵∠BCD+∠BOC=90°,∠BOC=∠AOK,
∴∠AOK+∠BAE=90°,
∴∠AKO=90°,即AE⊥CD.
点评 本题以旋转为背景,主要考查了相似三角形的判定与性质,在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用.寻找相似三角形的一般方法是依据基本图形对图形进行分解、组合;或作辅助线构造相似三角形.


科目:初中数学 来源: 题型:解答题
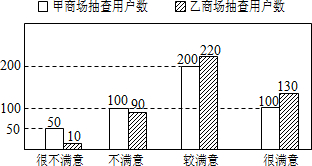 如图反映了被调查用户对甲,乙两种品牌空调售后服务的满意程度(以下称:用户满意度),分为很不满意,不满意,较满意,很满意,四个等级,并依次记为1分,2分,3分,4分.
如图反映了被调查用户对甲,乙两种品牌空调售后服务的满意程度(以下称:用户满意度),分为很不满意,不满意,较满意,很满意,四个等级,并依次记为1分,2分,3分,4分.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC依次进行轴对称(对称轴为y轴)、一次平移和以点O为位似中心进行位似变换得到△OA′B′.
如图,在Rt△ABC依次进行轴对称(对称轴为y轴)、一次平移和以点O为位似中心进行位似变换得到△OA′B′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
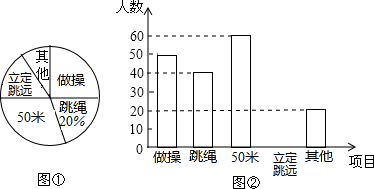 为了解某校八年级学生参加体育活动情况,从该校八年级学生中随机抽取了部分学生的体育活动自选项目进行统计,并根据调查结果绘制了如下两个统计图,请根据图中信息,回答下列问题:(1)本次调查共抽取了200名学生;
为了解某校八年级学生参加体育活动情况,从该校八年级学生中随机抽取了部分学生的体育活动自选项目进行统计,并根据调查结果绘制了如下两个统计图,请根据图中信息,回答下列问题:(1)本次调查共抽取了200名学生;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
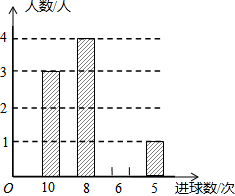 某校九年级学生在一节体育课中,选一组学生进行投篮比赛,每人投10次,汇总投进球数的情况进行统计分析,绘制了如下不完整的统计表和统计图.
某校九年级学生在一节体育课中,选一组学生进行投篮比赛,每人投10次,汇总投进球数的情况进行统计分析,绘制了如下不完整的统计表和统计图.| 次数 | 10 | 8 | 6 | 5 |
| 人数 | 3 | a | 2 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com