
 ).将△AOC绕AC的中点旋转180°,点O落到点B的位置,抛物线y=ax2-2
).将△AOC绕AC的中点旋转180°,点O落到点B的位置,抛物线y=ax2-2 x经过点A,点D是该抛物线的顶点.
x经过点A,点D是该抛物线的顶点.
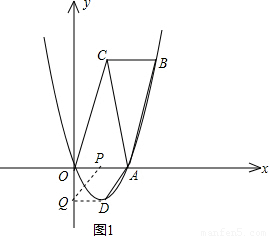


 ),根据A,D的坐标可求出直线AD的解析式为y=
),根据A,D的坐标可求出直线AD的解析式为y=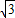 x-2
x-2 ,由于QP∥AD,因此直线PQ的解析式为y=
,由于QP∥AD,因此直线PQ的解析式为y= x+
x+ ,可求得P点的坐标为(-1,0).
,可求得P点的坐标为(-1,0). (1)证明:∵△AOC绕AC的中点旋转180°,
(1)证明:∵△AOC绕AC的中点旋转180°, x经过点A,
x经过点A, ,
, .
. x2-2
x2-2 x.
x. ),
), ).
). ×32-2
×32-2 ×3=3
×3=3 .
. ).
). ,tan∠DAF=
,tan∠DAF= ,
, ,
, ,
, .
. ,0).
,0).

科目:初中数学 来源:2007年全国中考数学试题汇编《二次函数》(07)(解析版) 题型:解答题
 ).将△AOC绕AC的中点旋转180°,点O落到点B的位置,抛物线y=ax2-2
).将△AOC绕AC的中点旋转180°,点O落到点B的位置,抛物线y=ax2-2 x经过点A,点D是该抛物线的顶点.
x经过点A,点D是该抛物线的顶点.
查看答案和解析>>
科目:初中数学 来源:2007年浙江省绍兴市中考数学试卷(解析版) 题型:解答题
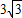 ).将△AOC绕AC的中点旋转180°,点O落到点B的位置,抛物线y=ax2-2
).将△AOC绕AC的中点旋转180°,点O落到点B的位置,抛物线y=ax2-2 x经过点A,点D是该抛物线的顶点.
x经过点A,点D是该抛物线的顶点.
查看答案和解析>>
科目:初中数学 来源:2007年全国中考数学试题汇编《图形的对称》(01)(解析版) 题型:选择题

查看答案和解析>>
科目:初中数学 来源:2007年全国中考数学试题汇编《四边形》(04)(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com