
分析 (1)一般用增长后的量=增长前的量×(1+增长率),2014年要投入教育经费是2000(1+x)万元,在2014年的基础上再增长x,就是2015年的教育经费数额,即可列出方程求解.
(2)利用(1)中求得的增长率来求2016年该地区将投入教育经费.
解答 解:(1)设该地区投入教育经费的年平均增长率为x,根据题意得:
2000(1+x)2=2420,
解得:x=0.1=10%,或x=-2.1(不合题意舍去).
答:该地区投入教育经费的年平均增长率为10%.
(2)根据题意得:
2420×(1+10%)=2662(万元),
答:2016年该地区将投入教育经费2662万元.
点评 本题考查了一元二次方程中增长率的知识.掌握增长前的量×(1+年平均增长率)年数=增长后的量是本题的关键.


科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 水位变化 | -5 | +7 | -3 | +4 | +10 | -9 | -20 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
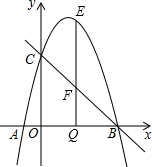 如图,直线y=-x+3与x轴交于B点,与y轴交于点C,抛物线y=-x2+bx+c经过B、C两点,且与x轴交于另一点A(A在B的左边).
如图,直线y=-x+3与x轴交于B点,与y轴交于点C,抛物线y=-x2+bx+c经过B、C两点,且与x轴交于另一点A(A在B的左边).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,有一矩形养鸡场,养鸡场的一边靠墙,墙长a米,另三边用篱笆围起来,篱笆总长48米,平行于墙的一边开一个2米宽的门.
如图所示,有一矩形养鸡场,养鸡场的一边靠墙,墙长a米,另三边用篱笆围起来,篱笆总长48米,平行于墙的一边开一个2米宽的门.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
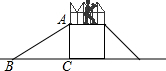 如图为某公园(六•一)前新增设的一台滑梯截面,已知该滑梯高度AC=2m,滑梯着地点B与梯架之间的距离BC=4m.
如图为某公园(六•一)前新增设的一台滑梯截面,已知该滑梯高度AC=2m,滑梯着地点B与梯架之间的距离BC=4m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线l1,l2交于点A,直线l2与x轴、y轴分别交于点B(-4,0)、D(0,4),直线l1所对应的函数关系式为y=-2x-2.
如图,直线l1,l2交于点A,直线l2与x轴、y轴分别交于点B(-4,0)、D(0,4),直线l1所对应的函数关系式为y=-2x-2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com