
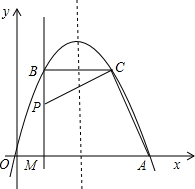
 如图,经过原点的抛物线y=-x2+mx(m>2)与x轴的另一交点为A,过点P(1,$\frac{m}{2}$)作直线PM⊥x轴于点M,交抛物线于点B.点B关于抛物线对称轴的对称点为C.连接CB,CP,CA,要使得CA⊥CP,则m的值为3.
如图,经过原点的抛物线y=-x2+mx(m>2)与x轴的另一交点为A,过点P(1,$\frac{m}{2}$)作直线PM⊥x轴于点M,交抛物线于点B.点B关于抛物线对称轴的对称点为C.连接CB,CP,CA,要使得CA⊥CP,则m的值为3. 分析 过点C作CD⊥x轴于点D,可以证得∠BCP=∠DCA,进而可得△CBP∽△CDA,利用△CBP∽△CDA得到对应边的比相等,即可求出m的值.
解答 解:如图,过点C作CD⊥x轴于点D,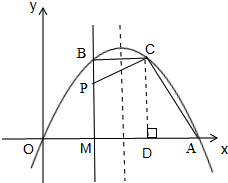
∵∠BCP+∠PCD=90°,∠DCA+∠PCD=90°,
∴∠BCP=∠DCA,
又∵∠CBP=∠CDA=90°
∴△CBP∽△CDA
∴$\frac{CD}{BC}=\frac{DA}{BP}$
在y=-x2+mx中,
令x=1,则y=m-1
∴B(1,m-1)
又∵对称轴x=$-\frac{m}{2×(-1)}=\frac{m}{2}$
∴BC=2($\frac{m}{2}$-1)=m-2,
∴C(m-1,m-1),
∴CD=m-1,BC=m-2,DA=OM=1,BP=$\frac{m}{2}$-1,
∴$\frac{m-1}{m-2}=\frac{1}{\frac{m}{2}-1}$,
∴m=3.
故答案为:3.
点评 本题主要考查二次函数的综合题,解题的关键是做出辅助线,利用数形结合证得△CBP∽△CDA.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
 如图,在正方形ABCD中,E是BC的中点,F是CD上一点,AE⊥EF,则下列结论中正确的结论有( )
如图,在正方形ABCD中,E是BC的中点,F是CD上一点,AE⊥EF,则下列结论中正确的结论有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在下面的网络图中,按要求画出图形,并回答问题:
如图,在下面的网络图中,按要求画出图形,并回答问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,二次函数y=-$\frac{\sqrt{3}}{3}{x}^{2}-\frac{2}{3}\sqrt{3}x+\sqrt{3}$的图象交x轴于A,B两点,交y轴于点C,顶点为D.
如图,二次函数y=-$\frac{\sqrt{3}}{3}{x}^{2}-\frac{2}{3}\sqrt{3}x+\sqrt{3}$的图象交x轴于A,B两点,交y轴于点C,顶点为D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知抛物线y=-$\frac{1}{4}$x2+bx+c与x轴交于A、B两点,与y轴交于点C,连结AC,BC,D是线段OB上一动点,以CD为一边向右作正方形CDEF,连结BF.若S△OBC=8,AC=BC.
已知抛物线y=-$\frac{1}{4}$x2+bx+c与x轴交于A、B两点,与y轴交于点C,连结AC,BC,D是线段OB上一动点,以CD为一边向右作正方形CDEF,连结BF.若S△OBC=8,AC=BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com