
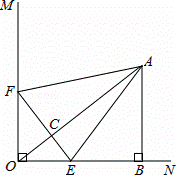
��ͼ����֪��MON=90�㣬A�ǡ�MON�ڲ���һ�㣬����A��AB��ON������Ϊ��B��AB=3���ף�OB=4���ף�����E��Fͬʱ��O���������E��1.5����/����ٶ���ON�����˶�����F��2����/����ٶ���OM�����˶���EF��OA���ڵ�C������AE������E�����Bʱ����F��ֹ֮ͣ�˶������˶�ʱ��Ϊt�루t��0����
��1����t=1��ʱ����EOF���ABO�Ƿ����ƣ���˵�����ɣ�
��2�����˶������У�����tȡ��ֵʱ������EF��OA��Ϊʲô��
�� 3������AF�����˶������У��Ƿ����ijһʱ��t��ʹ��S��AEF=
3������AF�����˶������У��Ƿ����ijһʱ��t��ʹ��S��AEF= S�ı���ABOF�������ڣ��������ʱt��ֵ���������ڣ���˵�����ɣ�
S�ı���ABOF�������ڣ��������ʱt��ֵ���������ڣ���˵�����ɣ�

�⣺��1����t=1��
��OE=1.5���ף�OF=2���ף�
��AB=3���ף�OB=4���ף�
��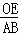 =
=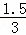 =
= ��
�� =
=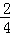 =
=
�ߡ�MON=��ABE=90�㣬
���EOF�ס�ABO��
��2�����˶������У�OE=1.5t��OF=2t��
��AB=3��OB=4��
��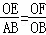 ��
��
�֡ߡ�EOF=��ABO=90�㣬
��Rt��EOF��Rt��ABO��
���AOB=��EOF��
�ߡ�AOB+��FOC=90�㣬
���EOF+��FOC=90�㣬
��EF��OA��
��3����ͼ������AF��
��OE=1.5t��OF=2t��
��BE=4��1.5t
��S��FOE=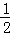 OE•OF=
OE•OF=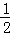 ��1.5t��2t=
��1.5t��2t=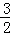 t2��S��ABE=
t2��S��ABE=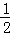 ����
���� 4��1.5t����3=6��
4��1.5t����3=6�� t��
t��
S����ABOF=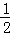 ��2t+3����4=4t+6
��2t+3����4=4t+6
��S��AEF=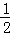 S�ı���ABOF
S�ı���ABOF
��S��FOE+S��ABE=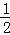 S����ABOF��
S����ABOF��
��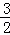 t2+6��
t2+6��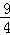 t=
t=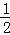 ��4t+6������6t2��17t+12=0��
��4t+6������6t2��17t+12=0��
���t=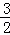 ��t=
��t=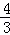 ��
��
�൱t=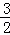 ��t=
��t=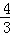 ʱ��S��AEF=
ʱ��S��AEF= S�ı���ABOF��
S�ı���ABOF��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ���ھ���ABCD�У���EΪAB���е㣬EF��EC��AD�ڵ�F������CF��AD��AE�������н��ۣ�
�١�AEF=��BCE��
��AF+BC��CF��
��S��CEF=S��EAF+S��CBE��
���� =
= �����CEF�ա�CDF��
�����CEF�ա�CDF��
������ȷ�Ľ���������������д������ȷ���۵���ţ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��֪x=2��y=-3�Ƕ�Ԫһ�η���5x+my+2=0�Ľ⣬��m��ֵΪ����������
| A��4 | B����4���� | C�� | �ģ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��֪�߶Σ��µĶ˵������ǣ���3��4�� ���£���2��3������������ƽ��5����λ����˵���
���£���2��3������������ƽ��5����λ����˵��� ��ֱ�Ϊ������������
��ֱ�Ϊ������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ����������a��b����ƽ�У���A��B�ǺӰ�a�ϵ������������C��D�ǺӰ�b�ϵ����㣬A��B�ľ���ԼΪ200�ף�ij���ںӰ�b�ϵĵ�P����á�APC=75�㣬��BPD=30�㣬������Ŀ���ԼΪ�����ף�
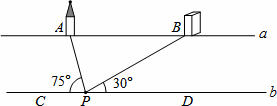
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com