
【题目】已知(x+3)2与|y﹣2|互为相反数,z是绝对值最小的有理数,求(x+y)y+xyz的值.
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
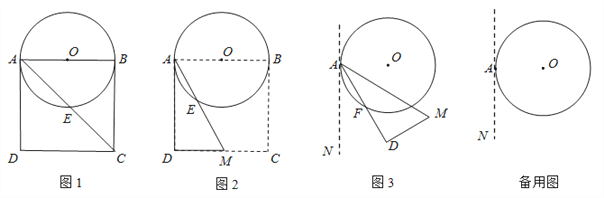
【题目】如图1,以边长为8的正方形纸片ABCD的边AB为直径作⊙O,交对角线AC于点E.
(1)线段AE=____________;
(2)如图2,以点A为端点作∠DAM=30°,交CD于点M,沿AM将四边形ABCM剪掉,使Rt△ADM绕点A逆时针旋转(如图3),设旋转角为α(0°<α<150°),旋转过程中AD与⊙O交于点F.
①当α=30°时,请求出线段AF的长;
②当α=60°时,求出线段AF的长;判断此时DM与⊙O的位置关系,并说明理由;
③当α=___________°时,DM与⊙O相切。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据所学知识填空. 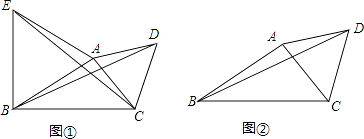
(1)如图①,△ABE,△ACD都是等边三角形,若CE=6,则BD的长=;
(2)如图②,△ABC中,∠ABC=30°,AB=3,BC=4,D是△ABC外一点,且△ACD是等边三角形,则BD的长= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AE∥BF,AC平分∠BAD,交BF于点C,BD平分∠ABC,交AE于点D,连接CD. 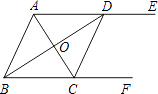
(1)若AB=1,则BC的长=;
(2)求证:四边形ABCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在解答“分解因式:(1)3x2-9x+3;(2)4x2-9.”时,是这样做的:
解:(1)3x2-9x+3=3(x2-6x+1);
(2)4x2-9=(2x+3)(2x-3).
请你利用分解因式与整式乘法的关系,判断他分解得对不对.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com