
分析 首先化简二次根式,进而将已知代入求出答案.
解答 解:∵a+b=-5,ab=2,
∴b$\sqrt{\frac{b}{a}}$+a$\sqrt{\frac{a}{b}}$=-b•$\frac{\sqrt{ab}}{a}$-$\frac{a\sqrt{ab}}{b}$
=-$\frac{{b}^{2}+{a}^{2}}{ab}$$\sqrt{ab}$
=-$\frac{(a+b)^{2}-2ab}{ab}$$\sqrt{ab}$
=-$\frac{25-2×2}{2}$$\sqrt{2}$
=-$\frac{21}{2}$$\sqrt{2}$.
故答案为:-$\frac{21}{2}$$\sqrt{2}$.
点评 此题主要考查了二次根式的加减运算,正确化简二次根式是解题关键.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
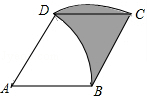 菱形ABCD的边长为2$\sqrt{3}$m,∠A=60°,弧CD是以点B为圆心,BC长为半径的弧,弧BD是以A为圆心,AB长为半径的弧,则阴影部分面积为3$\sqrt{3}$m2.(结果保留根号)
菱形ABCD的边长为2$\sqrt{3}$m,∠A=60°,弧CD是以点B为圆心,BC长为半径的弧,弧BD是以A为圆心,AB长为半径的弧,则阴影部分面积为3$\sqrt{3}$m2.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
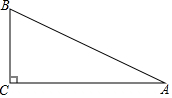 已知:如图,Rt△ABC中,∠C=90°,AC=$\sqrt{3}$-$\sqrt{2}$,BC=$\sqrt{3}$+$\sqrt{2}$,求
已知:如图,Rt△ABC中,∠C=90°,AC=$\sqrt{3}$-$\sqrt{2}$,BC=$\sqrt{3}$+$\sqrt{2}$,求查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com